 par un diagramme de Voronoi 2D discret défini
par les centres
par un diagramme de Voronoi 2D discret défini
par les centres
 où
où
Nous avons vu dans la section 6.4.5 que le
calcul de la fonction pouvait être réalisé à l'aide d'un
diagramme de Voronoi 3D discret. Les principales limitations de cette
méthode viennent du pré-calcul de la couleur représentative de
chaque couleur de l'espace . Les travaux menés par
Otha [OKS80] et confirmés par nos propres expérimentations
montrent que l'essentiel de l'information d'une image naturelle (par
opposition à une image de synthèse) est contenu dans le plan
vectoriel ![]() défini par les deux premiers vecteurs propres
de la matrice de covariance de l'image. Le plan
défini par les deux premiers vecteurs propres
de la matrice de covariance de l'image. Le plan ![]() nous
permet donc d'approximer efficacement l'ensemble des couleurs de
l'image. De plus, la matrice de passage de l'espace de couleurs à
l'espace des vecteurs propres étant une matrice orthogonale, les
calculs de distances effectués dans l'espace des vecteurs propres
seront similaires aux calculs de distances effectués dans l'espace
de couleur initial. Il est donc possible d'approximer de manière
efficace le diagramme de Voronoi 3D discret de centres
nous
permet donc d'approximer efficacement l'ensemble des couleurs de
l'image. De plus, la matrice de passage de l'espace de couleurs à
l'espace des vecteurs propres étant une matrice orthogonale, les
calculs de distances effectués dans l'espace des vecteurs propres
seront similaires aux calculs de distances effectués dans l'espace
de couleur initial. Il est donc possible d'approximer de manière
efficace le diagramme de Voronoi 3D discret de centres
 par un diagramme de Voronoi 2D discret défini
par les centres
par un diagramme de Voronoi 2D discret défini
par les centres
 où
où ![]() représente
la projection de la couleur représentative
représente
la projection de la couleur représentative ![]() sur le plan
sur le plan
![]() . Cette projection est définie par les équations
suivantes :
. Cette projection est définie par les équations
suivantes :
L'utilisation d'un diagramme de Voronoi 2D discret impose de
délimiter le domaine sur lequel les calculs de distances d'un point
![]() aux centres
aux centres
 seront effectués. A
cette fin, nous calculons la boite englobante des projections
seront effectués. A
cette fin, nous calculons la boite englobante des projections ![]() des couleurs de l'image sur le plan
des couleurs de l'image sur le plan ![]() . Le calcul de cette
boite englobante s'effectue en déterminant les valeurs
. Le calcul de cette
boite englobante s'effectue en déterminant les valeurs
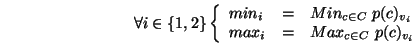 et
et
![]() définies par :
définies par :
Le calcul du diagramme de Voronoi 2D discret peut alors s'effectuer en
allouant une image de taille
![]() et en
affectant à chaque point discret de l'image l'indice de son centre
le plus proche parmis les points
et en
affectant à chaque point discret de l'image l'indice de son centre
le plus proche parmis les points
 . Cette
initialisation du diagramme de Voronoi 2D discret est effectuée
grâce à la méthode incrémentale de
Danielson [Dan80] de complexité
|V_I| où
. Cette
initialisation du diagramme de Voronoi 2D discret est effectuée
grâce à la méthode incrémentale de
Danielson [Dan80] de complexité
|V_I| où ![]() représente la taille du diagramme de
Voronoi 2D discret associé à I.
représente la taille du diagramme de
Voronoi 2D discret associé à I.
Le calcul du diagramme ![]() impose donc de parcourir une fois l'image
pour calculer les deux vecteurs propres
impose donc de parcourir une fois l'image
pour calculer les deux vecteurs propres ![]() et
et ![]() , puis de
reparcourir celle ci afin de déterminer les points
, puis de
reparcourir celle ci afin de déterminer les points
![]() et
et
![]() . La compléxité totale du calcul du diagramme
. La compléxité totale du calcul du diagramme
![]() est donc égale à 2|I| + |V_I|.
est donc égale à 2|I| + |V_I|.
Le diagramme de Voronoi ![]() associé à une image
associé à une image ![]() nous permet
donc d'approximer le calcul de la fonction définie dans la
section 6.4.1. Un algorithme utilisant cette
approximation pour réaliser l'inversion de la table de couleurs est
donné sur la figure 4.
nous permet
donc d'approximer le calcul de la fonction définie dans la
section 6.4.1. Un algorithme utilisant cette
approximation pour réaliser l'inversion de la table de couleurs est
donné sur la figure 4.
L'utilisation d'un diagramme de Voronoi 2D discret induit deux types
d'approximation : Une approximation due à la projection de
l'ensemble des donnés 3D de l'image sur le plan ![]() et une
approximation due à la discrétisation du plan
et une
approximation due à la discrétisation du plan ![]() pour
calculer le diagramme de Voronoi 2D. Du fait de ces deux
approximations l'algorithme 4 est suceptible de renvoyer
un indice différent de celui fourni par la fonction
. Toutefois, les erreurs dues aux approximations induisant de petites
erreurs pour le calcul des distances, les erreurs commises par
l'algorithme 4 se situent souvent entre deux indices
dont les cellules sont adjacentes. Afin de supprimer ce type d'erreur
nous déterminons durant le calcul de
pour
calculer le diagramme de Voronoi 2D. Du fait de ces deux
approximations l'algorithme 4 est suceptible de renvoyer
un indice différent de celui fourni par la fonction
. Toutefois, les erreurs dues aux approximations induisant de petites
erreurs pour le calcul des distances, les erreurs commises par
l'algorithme 4 se situent souvent entre deux indices
dont les cellules sont adjacentes. Afin de supprimer ce type d'erreur
nous déterminons durant le calcul de ![]() le diagramme de Delaunay
le diagramme de Delaunay
![]() associé à
associé à ![]() . Ces deux structures sont alors combinées
de la façon suivante. Soit
. Ces deux structures sont alors combinées
de la façon suivante. Soit ![]() l'indice de la cellule
contenant la projection de
l'indice de la cellule
contenant la projection de ![]() . L'utilisation du diagramme de Delaunay
nous permet d'acceder à la structure
. L'utilisation du diagramme de Delaunay
nous permet d'acceder à la structure
![]() contenant
l'ensemble des cellules adjacentes à
contenant
l'ensemble des cellules adjacentes à ![]() . L'utilisation du
nouveau diagramme
. L'utilisation du
nouveau diagramme ![]() nous permet d'affecter à
nous permet d'affecter à ![]() la couleur la
plus proche de celui-ci parmis l'ensemble des couleurs
représentatives dont l'indice appartient à
la couleur la
plus proche de celui-ci parmis l'ensemble des couleurs
représentatives dont l'indice appartient à
![]() . Ceci
définit une nouvelle fonction
. Ceci
définit une nouvelle fonction ![]() donnée par l'équation :
donnée par l'équation :
Un algorithme utilisant le diagramme de Delaunay ![]() et la fonction
et la fonction
![]() pour inverser la table de couleurs d'une image est
représenté sur la figure 5.
pour inverser la table de couleurs d'une image est
représenté sur la figure 5.
La complexité moyenne de la fonction ![]() est déterminée
par le nombre moyen de cellules adjacentes à une cellule
donnée. Les travaux d'Etienne Bertin [Ber94] ont montré
que le nombre moyen d'arrêtes d'une cellule de Voronoi est
indépendant du nombre de germes et approximativement égal à
est déterminée
par le nombre moyen de cellules adjacentes à une cellule
donnée. Les travaux d'Etienne Bertin [Ber94] ont montré
que le nombre moyen d'arrêtes d'une cellule de Voronoi est
indépendant du nombre de germes et approximativement égal à
![]() .
algo-inv1Premier approche pour l'inversion de la tables de couleurs. Les symboles
.
algo-inv1Premier approche pour l'inversion de la tables de couleurs. Les symboles ![]() et
et ![]() représentent respectivement la couleur du pixel
représentent respectivement la couleur du pixel ![]() et l'indice de la cellule de Voronoï contenant
et l'indice de la cellule de Voronoï contenant ![]() . La projection sur le plan
. La projection sur le plan ![]() est notée
est notée ![]() .
algo-inv2Second algorithme d'inversion de tables de couleurs. Les symboles
.
algo-inv2Second algorithme d'inversion de tables de couleurs. Les symboles ![]() et
et ![]() représentent respectivement la couleur du pixel
représentent respectivement la couleur du pixel ![]() et l'indice de la cellule de Voronoi contenant
et l'indice de la cellule de Voronoi contenant ![]() .La projection sur le plan
.La projection sur le plan ![]() est notée
est notée ![]() .
.