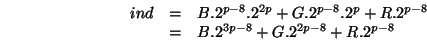 nous donnent respectivement les numéros
d'intervalles sur les axes
nous donnent respectivement les numéros
d'intervalles sur les axes 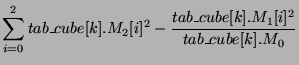 carrés, le
numéro d'un sous cube est:
carrés, le
numéro d'un sous cube est:
La quantité
![]() nous donne le numéro de l'intervalle
sur l'axe
nous donne le numéro de l'intervalle
sur l'axe ![]() . De même, les quantités
. De même, les quantités
![]() et
et
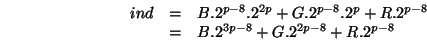 nous donnent respectivement les numéros
d'intervalles sur les axes
nous donnent respectivement les numéros
d'intervalles sur les axes ![]() et
et ![]() . Compte tenu de notre
numérotation et sachant que le plan
. Compte tenu de notre
numérotation et sachant que le plan ![]() comporte
comporte 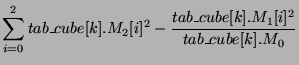 carrés, le
numéro d'un sous cube est:
carrés, le
numéro d'un sous cube est:
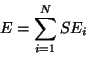
init_partition(const image &I, int p)
{
unsigned char couleur[3];
int N=(1<<3*p);
sous_cube * tab_cube = new sous_cube[N];
I.debut();
do
{
I.lire_pixel(couleur);
int ind =couleur[2]*2^(3*p-8)+couleur[1]*2^(2*p-8)+couleur[0]*2^(p-8)
tab_cube[ind].M0++;
for(int i =0;i<3;i++)
{
tab_cube[ind].M1[i] += couleur[i];
tab_cube[ind].M2[i] += couleur[i]*couleur[i];
}
}
while(I.suivant());
}
Le nombre de couleurs de l'image résultat sera égal à ![]() si tous les
sous cubes contiennent au moins une couleur. En pratique, on trouve
généralement des valeurs bien inférieures à
si tous les
sous cubes contiennent au moins une couleur. En pratique, on trouve
généralement des valeurs bien inférieures à ![]() .
.
L'expression de l'erreur quadratique du cluster ![]() se trouve dans le
cours et est égale à:
se trouve dans le
cours et est égale à:
L'erreur quadratique de partition avant la fusion est donnée par:
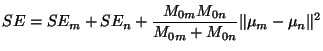
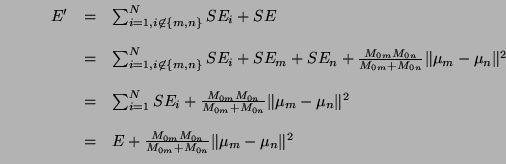 et
et L'erreur quadratique de partition après la fusion est donc égale à:
void merge_sous_cubes(sous_cube * tab_cube, int i,int j)
{
int max = MAX(i,j);
int min = MIN(i,j);
tab_cube[min].pere = max;
tab_cube[max].MO+=tab_cube[min].MO;
for(int i=0;i<3;i++)
{
tab_cube[max].M1[i] += tab_cube[min].M1[i];
tab_cube[max].M2[i] += tab_cube[min].M2[i];
}
}
void give_mean(sous_cube * tab_cube, unsigned int* color,unsigned int* moyenne,int p)
{
int ind =couleur[2]<<(3*p-8)+couleur[1]<<(2*p-8)+couleur[0]<<(p-8);
while (ind != tab_cube[ind].pere)
ind = tab_cube[ind].pere;
for(int i=0;i<3;i++)
moyenne[i] = tab_cube[ind].M1[i]/tab_cube.M0;
}
La suppression des indirections peut s'effectuer grâce à une simple boucle descendante du type suivant:
for(int i=N-1;i>0;i--)
{
int ind =tab_cube[i].pere;
tab_cube[i].pere= tab_cube[ind].pere;
}
qui positionne le père de chaque sous cube au père de son père. Etant
donné que les relations père-fils vont toujours de l'indice le plus
petit vers l'indice le plus grand, la boucle descendante supprime
toutes les indirections en une passe.