suivant: Définition d'un espace couleur
monter: Exercices
précédent: Questions de compréhension
Table des matières
Index
Conversion entre espaces couleurs
On désigne par
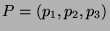 et
et
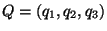 deux systèmes de
primaires.
deux systèmes de
primaires.
- Justifiez en quelques phrases, l'existence pour tout
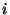 appartenant
à
appartenant
à 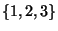 d'un unique triplet
d'un unique triplet
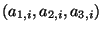 tel que
:
tel que
:
- Soit
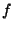 un spectre quelconque. On désigne par
un spectre quelconque. On désigne par
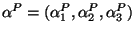 et
et
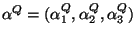 les coordonnées
associées au spectre
les coordonnées
associées au spectre 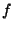 dans les systèmes
dans les systèmes 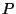 et
et 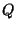 . On a donc:
Montrez que :
Cette matrice est appelée la matrice de conversion de l'espace
. On a donc:
Montrez que :
Cette matrice est appelée la matrice de conversion de l'espace 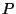 à
l'espace
à
l'espace 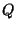 .
.
Brun Luc
2004-03-25
![]() et
et
![]() deux systèmes de
primaires.
deux systèmes de
primaires.