




suivant: Correction des Exercices
monter: Exercices
précédent: Définition d'un espace couleur
Table des matières
Index
Donné un nombre réel 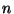 , on désigne par
, on désigne par 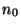 , sa valeur entière
inférieure, et
, sa valeur entière
inférieure, et 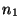 sa valeur entière supérieure. Le point
sa valeur entière supérieure. Le point 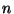 est
donc compris dans le segment
est
donc compris dans le segment
![$ [n_0 ,n_1]$](img627.png) (figure 4.12). De
même, un point de coordonnées
(figure 4.12). De
même, un point de coordonnées 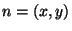 est compris entre
est compris entre 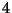 points
(
points
(
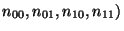 . Dans ce cas,
. Dans ce cas, 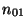 désigne le
point de coordonnées entière
désigne le
point de coordonnées entière
![$ ([x],[y]+1)$](img632.png) où
où ![$ [x]$](img633.png) est la partie
entière inférieure. Ce schéma ce généralise en
est la partie
entière inférieure. Ce schéma ce généralise en 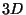 où un point est
inclus dans un cube défini par
où un point est
inclus dans un cube défini par 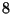 points
points 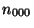 à
à 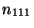 (figure 4.13).
(figure 4.13).
En dimension 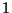 (figure 4.12(a)) : On suppose que
(figure 4.12(a)) : On suppose que 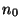 et
et
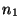 sont associés à des valeurs
sont associés à des valeurs 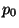 et
et 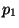 . La valeur
. La valeur 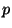 associée à
associée à 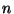 peut être définie par interpolation linéaire. Si l'on
appelle cette fonction
peut être définie par interpolation linéaire. Si l'on
appelle cette fonction 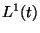 on a :
on a :
interpoInterpolation en dimensions 1 et 2
- En dimension 2 (figure 4.12(b)) : Chaque point
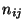 est associé à une valeur
est associé à une valeur 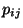 . Donnez la valeur
. Donnez la valeur 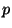 associée à
associée à 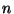 en fonction de
en fonction de 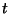 et
et 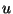 .
La fonction obtenue s'appellera
.
La fonction obtenue s'appellera 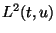 .
.
- En dimension 3(figure 4.13) : On désigne par
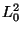 l'interpolation bilinéaire sur le rectangle
l'interpolation bilinéaire sur le rectangle
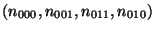 et par
et par 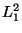 l'interpolation
bilinéaire sur le rectangle
l'interpolation
bilinéaire sur le rectangle
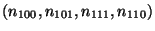 .
. 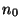 et
et 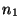 représentent la projection de
représentent la projection de 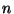 sur chacun de ces
rectangles. Donnez la valeur de
sur chacun de ces
rectangles. Donnez la valeur de 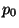 et
et 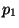 en utilisant
en utilisant 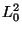 et
et
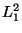 . Déduisez en la valeur
. Déduisez en la valeur 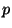 de
de 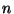 à l'aide d'une interpolation
linéaire entre
à l'aide d'une interpolation
linéaire entre 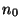 et
et 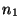 . La fonction s'appellera
. La fonction s'appellera
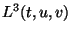 .
.
interpo3DInterpolation 3D
On suppose que l'on a trois tableaux de float 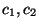 et
et 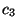 de
taille
de
taille
![$ [32][32][32]$](img654.png) . L'entrée
. L'entrée
![$ c_l[i][j][k]$](img655.png) code la composante
code la composante 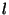 de la transformée du triplé
de la transformée du triplé 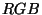
 dans un espace
couleur donné.
dans un espace
couleur donné.
- A t'on calculé la transformée de tous les triplés
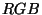 ? Pourquoi ?
? Pourquoi ?
- Utilisez les question précédentes pour déduire la transformée de
tout triplé
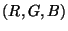 .On donnera pour cela :
.On donnera pour cela :
- Si l'on doit calculer les tableaux
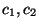 et
et 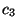 au début
de l'algorithme, cette méthode est elle efficace pour calculer la
transformée des couleurs d'une image
au début
de l'algorithme, cette méthode est elle efficace pour calculer la
transformée des couleurs d'une image
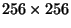 ? Proposez une
solution (simple).
? Proposez une
solution (simple).





suivant: Correction des Exercices
monter: Exercices
précédent: Définition d'un espace couleur
Table des matières
Index
Brun Luc
2004-03-25
![]() , on désigne par
, on désigne par ![]() , sa valeur entière
inférieure, et
, sa valeur entière
inférieure, et ![]() sa valeur entière supérieure. Le point
sa valeur entière supérieure. Le point ![]() est
donc compris dans le segment
est
donc compris dans le segment
![]() (figure 4.12). De
même, un point de coordonnées
(figure 4.12). De
même, un point de coordonnées ![]() est compris entre
est compris entre ![]() points
(
points
(
![]() . Dans ce cas,
. Dans ce cas, ![]() désigne le
point de coordonnées entière
désigne le
point de coordonnées entière
![]() où
où ![]() est la partie
entière inférieure. Ce schéma ce généralise en
est la partie
entière inférieure. Ce schéma ce généralise en ![]() où un point est
inclus dans un cube défini par
où un point est
inclus dans un cube défini par ![]() points
points ![]() à
à ![]() (figure 4.13).
(figure 4.13).
![]() (figure 4.12(a)) : On suppose que
(figure 4.12(a)) : On suppose que ![]() et
et
![]() sont associés à des valeurs
sont associés à des valeurs ![]() et
et ![]() . La valeur
. La valeur ![]() associée à
associée à ![]() peut être définie par interpolation linéaire. Si l'on
appelle cette fonction
peut être définie par interpolation linéaire. Si l'on
appelle cette fonction ![]() on a :
on a :
![]() et
et ![]() de
taille
de
taille
![]() . L'entrée
. L'entrée
![]() code la composante
code la composante ![]() de la transformée du triplé
de la transformée du triplé ![]()
![]() dans un espace
couleur donné.
dans un espace
couleur donné.