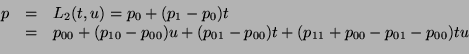suivant: Cas de la dimension
monter: Optimisation des transformations
précédent: Optimisation des transformations
Table des matières
Index
Les valeurs de 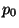 et
et 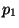 respectivement associées à
respectivement associées à 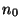 et
et
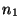 se déduisent par une interpolation
se déduisent par une interpolation 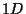 .
.
où 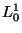 et
et 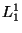 correspondent respectivement aux interpolations
sur les segments
correspondent respectivement aux interpolations
sur les segments
![$ [n_{00},n_{10}]$](img691.png) et
et
![$ [n_{01},n_{11}]$](img692.png) .
.
On en déduit la valeur 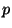 de
de 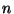 par interpolation
par interpolation 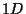 :
:
Brun Luc
2004-03-25
![]() et
et ![]() respectivement associées à
respectivement associées à ![]() et
et
![]() se déduisent par une interpolation
se déduisent par une interpolation ![]() .
.
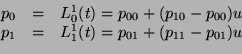
![]() de
de ![]() par interpolation
par interpolation ![]() :
: