




suivant: Sélection de la stratégie
monter: Étude détaillée de l'approche
précédent: Étude détaillée de l'approche
Table des matières
Index
Les approches
descendantes ont quant
à elles été beaucoup plus
explorées [Hec82,WWP88,WZ91,Wu92,BBA94]. Ces
méthodes initialisent un multi-ensemble à partir de
l'image et partitionnent celui-ci jusqu'à obtenir 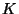 multi-ensembles formant une partition de . Comme nous l'avons
vu dans la section 5.2.1, trouver le
partitionnement idéal en
multi-ensembles formant une partition de . Comme nous l'avons
vu dans la section 5.2.1, trouver le
partitionnement idéal en 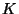 multi-ensembles minimisant l'équation
de la définition 6 est un problème complet pour
des images couleurs. Selon Anderberg [And73], le nombre de
partitionnements possibles est égal à
multi-ensembles minimisant l'équation
de la définition 6 est un problème complet pour
des images couleurs. Selon Anderberg [And73], le nombre de
partitionnements possibles est égal à
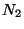 où
où 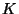 est le
nombre final de couleurs et le multi-ensemble associé à
l'image. L'algorithme trivial testant chaque partitionnement n'est
donc pas réaliste et des heuristiques de découpe doivent être
employées. Balasubramanian [BBA94] réalise un histogramme
1-D suivant une des composantes de l'image (voir
définition 7) puis partitionne par des plans
perpendiculaires à cet axe en
est le
nombre final de couleurs et le multi-ensemble associé à
l'image. L'algorithme trivial testant chaque partitionnement n'est
donc pas réaliste et des heuristiques de découpe doivent être
employées. Balasubramanian [BBA94] réalise un histogramme
1-D suivant une des composantes de l'image (voir
définition 7) puis partitionne par des plans
perpendiculaires à cet axe en 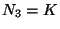 multi-ensembles. Il
sélectionne ensuite un autre axe de découpe, et redécoupe chaque
multi-ensemble perpendiculairement à cet axe à l'aide d'histogrammes 1D
calculés sur chacun des
multi-ensembles. Il
sélectionne ensuite un autre axe de découpe, et redécoupe chaque
multi-ensemble perpendiculairement à cet axe à l'aide d'histogrammes 1D
calculés sur chacun des 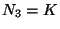 multi-ensembles. Il
obtient ainsi
multi-ensembles. Il
obtient ainsi 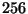 multi-ensembles. Une dernière itération de ce
processus fournit les
multi-ensembles. Une dernière itération de ce
processus fournit les 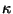 multi-ensembles finaux. Cette méthode
semble prometteuse mais laisse de nombreuses questions en
suspend. Tout d'abord on ne connaît pas, sauf à faire une
énumération exhaustive, la séquence optimale d'axes suivant
lesquels on doit réaliser le partitionnement. De plus, l'extension de
résultats valables pour
multi-ensembles finaux. Cette méthode
semble prometteuse mais laisse de nombreuses questions en
suspend. Tout d'abord on ne connaît pas, sauf à faire une
énumération exhaustive, la séquence optimale d'axes suivant
lesquels on doit réaliser le partitionnement. De plus, l'extension de
résultats valables pour 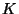 proche de l'infini à des valeurs de
proche de l'infini à des valeurs de
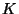 comprises entre
comprises entre 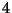 et
et 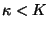 semble pour le moins
hasardeuse. Enfin, cet algorithme travaillant avec un ensemble
d'histogrammes 1D tient a priori moins compte de l'information 3D des
couleurs qu'un algorithme travaillant directement sur les données
3D. Une autre méthode présentée par Wu [Wu92] utilise la
programmation dynamique pour partitionner le multi-ensemble
en
semble pour le moins
hasardeuse. Enfin, cet algorithme travaillant avec un ensemble
d'histogrammes 1D tient a priori moins compte de l'information 3D des
couleurs qu'un algorithme travaillant directement sur les données
3D. Une autre méthode présentée par Wu [Wu92] utilise la
programmation dynamique pour partitionner le multi-ensemble
en 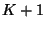 multi-ensembles (
multi-ensembles (
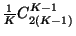 ). Les multi-ensembles
restants sont alors récursivement découpés en deux jusqu'à
obtenir les
). Les multi-ensembles
restants sont alors récursivement découpés en deux jusqu'à
obtenir les 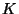 multi-ensembles finaux. Le problème dans ce cas est
de définir la valeur optimale de
multi-ensembles finaux. Le problème dans ce cas est
de définir la valeur optimale de 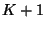 .
.
La plupart des algorithmes de quantification basés sur une approche
descendante [Hec82,WWP88,WZ91,Wu92,BBA94] initialisent
un multi-ensemble à partir de l'image et subdivisent
récursivement en deux jusqu'à obtenir 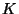 multi-ensembles
formant une partition de . Le découpage récursif consiste
à choisir un multi-ensemble parmi les multi-ensembles déjà
créés et à le découper en deux. Ce processus doit être
itéré
multi-ensembles
formant une partition de . Le découpage récursif consiste
à choisir un multi-ensemble parmi les multi-ensembles déjà
créés et à le découper en deux. Ce processus doit être
itéré 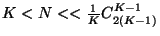 fois de façon à obtenir les
fois de façon à obtenir les 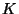 multi-ensembles
finaux. Le découpage de chaque multi-ensemble est réalisé par un
plan appelé plan de découpe orthogonal à une direction
appelée direction de découpe. Ce processus peut se
subdiviser en 4 étapes élémentaires communes à tous les
algorithmes de cette famille :
multi-ensembles
finaux. Le découpage de chaque multi-ensemble est réalisé par un
plan appelé plan de découpe orthogonal à une direction
appelée direction de découpe. Ce processus peut se
subdiviser en 4 étapes élémentaires communes à tous les
algorithmes de cette famille :
- La sélection d'une stratégie de découpe
- La sélection du multi-ensemble à découper
- La sélection d'une direction de découpe
- La recherche de la position du plan de coupe orthogonal à la direction de coupe.
Les heuristiques utilisées lors de ces 4 étapes nécessitent un
stockage approprié du multi-ensemble 3D associé à l'image. Nous
allons à présent étudier ces heuristiques et les structures de
données utilisées pour stocker le multi-ensemble associé à
l'image.





suivant: Sélection de la stratégie
monter: Étude détaillée de l'approche
précédent: Étude détaillée de l'approche
Table des matières
Index
Brun Luc
2004-03-25
![]() multi-ensembles
formant une partition de . Le découpage récursif consiste
à choisir un multi-ensemble parmi les multi-ensembles déjà
créés et à le découper en deux. Ce processus doit être
itéré
multi-ensembles
formant une partition de . Le découpage récursif consiste
à choisir un multi-ensemble parmi les multi-ensembles déjà
créés et à le découper en deux. Ce processus doit être
itéré ![]() fois de façon à obtenir les
fois de façon à obtenir les ![]() multi-ensembles
finaux. Le découpage de chaque multi-ensemble est réalisé par un
plan appelé plan de découpe orthogonal à une direction
appelée direction de découpe. Ce processus peut se
subdiviser en 4 étapes élémentaires communes à tous les
algorithmes de cette famille :
multi-ensembles
finaux. Le découpage de chaque multi-ensemble est réalisé par un
plan appelé plan de découpe orthogonal à une direction
appelée direction de découpe. Ce processus peut se
subdiviser en 4 étapes élémentaires communes à tous les
algorithmes de cette famille :