La méthode d'Heckbert [Hec82], basée sur une découpe
uniforme de l'espace de couleurs, permet de rejeter a priori des
couleurs représentatives qui ne peuvent réaliser le minimum de
l'équation (6.14). Heckbert effectue une découpe du cube
![]() en
en ![]() sous cubes. Chaque cube contient une liste de couleurs
représentatives pouvant être la couleurs représentative d'une couleur
du cube. Chaque liste est définie en calculant la distance
sous cubes. Chaque cube contient une liste de couleurs
représentatives pouvant être la couleurs représentative d'une couleur
du cube. Chaque liste est définie en calculant la distance ![]() entre
la couleur représentative la plus proche du centre du cube et le coin
du cube le plus éloigné de la couleur
représentative(Figure 6.8). Cette distance donne
une limite supérieure de la distance entre une couleur du cube et sa
couleur représentative. Donc toute couleur représentative dont la
distance au cube est plus grande que
entre
la couleur représentative la plus proche du centre du cube et le coin
du cube le plus éloigné de la couleur
représentative(Figure 6.8). Cette distance donne
une limite supérieure de la distance entre une couleur du cube et sa
couleur représentative. Donc toute couleur représentative dont la
distance au cube est plus grande que ![]() est rejetée de la liste.
est rejetée de la liste.
Les tests effectués par Heckbert [Hec82] montrent que le
nombre de tests nécessaires pour calculer l'image 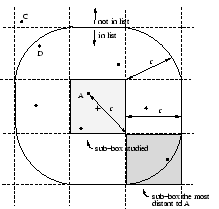 d'une
couleur
d'une
couleur ![]() est d'environ K23, où
est d'environ K23, où ![]() est le nombre
de couleurs représentatives. Cette méthode permet donc de diminuer la
complexité du calcul de la fonction
est le nombre
de couleurs représentatives. Cette méthode permet donc de diminuer la
complexité du calcul de la fonction ![]() sans toutefois changer
l'ordre de grandeur du temps de calcul de cette fonction.
sans toutefois changer
l'ordre de grandeur du temps de calcul de cette fonction.
|
|