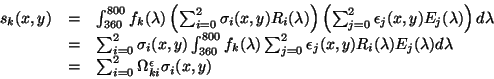suivant: Exercices
monter: Utilisation des spectres en
précédent: Utilisation des spectres en
Table des matières
Index
Utilisation des spectres en traitement d'images
L'utilisation des spectres en traitement d'image repose beaucoup sur
l'utilisation de la formule de Shafer (voir
section 2.2.5) et souvent sur une approximation de celle
ci pour les diélectriques qui consiste à négliger la composante
spéculaire. On obtient alors:
aussi bien pour les métaux que pour les diélectriques. La réponse du
capteur 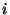 est alors donnée par:
est alors donnée par:
En traitement d'images, on cherche souvent à caractériser les objets
qui compose l'image soit pour les retrouver (segmentation) soit pour
les reconnaître (reconnaissance de formes). Dans cette perspective la
formule précédente présente deux inconvénients majeurs. En effet, La
réponse des capteurs dépend:
- de la géométrie de l'objet. Ceci induit des problèmes lorsque
l'on désire retrouver un objet indépendamment de sa géométrie.
- de l'illuminant. Si l'on désire caractériser un objet on
souhaiterais avoir une mesure indépendante des conditions
d'éclairages.
le premier problème peut être résolu en faisant le rapport des
coordonnées. En effet, si nous posons:
qui est un terme qui ne dépend pas de la géométrie de l'objet, l'on
obtient:
autrement dit, en dénotant 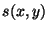 le vecteur couleur:
l'ensemble des couleurs associé a un seul matériaux parcourt donc une
droite de vecteur directeur
le vecteur couleur:
l'ensemble des couleurs associé a un seul matériaux parcourt donc une
droite de vecteur directeur
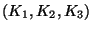 . La projection de cette
droite sur le plan
. La projection de cette
droite sur le plan
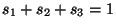 est égale à:
qui est un terme indépendant de la géométrie utilisé pour caractérisé
le matériau. Certains auteurs préfèrent la projection sur la sphère
unité donnée par:
est égale à:
qui est un terme indépendant de la géométrie utilisé pour caractérisé
le matériau. Certains auteurs préfèrent la projection sur la sphère
unité donnée par:
La résolution du second problème est connue dans la littérature sous le
nom de constance des couleurs. Ce problème assez complexe à résoudre
dans le cas général se simplifie grandement si l'on dispose d'un objet
de réflectance connue. Cette méthode suppose toutefois que l'on
projette l'illuminant et la fonction de réflectance sur une finie de
fonction ce qui induit une très forte approximation. On a alors:
où
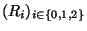 et
et
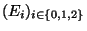 sont des bases
de fonctions permettant la décomposition de la réflectance
sont des bases
de fonctions permettant la décomposition de la réflectance 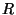 et
l'illuminant
et
l'illuminant 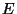 .
.
Donné ces équations la réponse d'un capteur 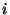 associé au pixel de
coordonnées
associé au pixel de
coordonnées 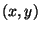 est donnée par une équation similaire à
l'équation 2.21:
est donnée par une équation similaire à
l'équation 2.21:
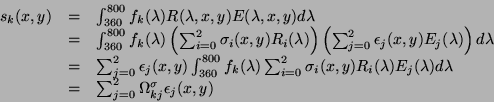 |
(2.22) |
avec
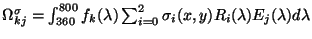
On obtient sous forme matricielle:
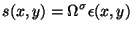 |
(2.23) |
Si nous plaçons dans la scène un objet de réflectance
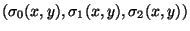 connue, la détermination
de l'illuminant revient simplement à inverser la matrice
connue, la détermination
de l'illuminant revient simplement à inverser la matrice
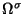 . On a de fait:
L'équation 2.22 peut également s'écrire sous la forme:
avec
. On a de fait:
L'équation 2.22 peut également s'écrire sous la forme:
avec
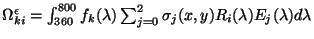
On obtient sous forme matricielle:
Si la valeur de 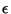 est donnée en tout point
est donnée en tout point 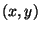 par la
formule 2.23 on obtient:
par la
formule 2.23 on obtient:





suivant: Exercices
monter: Utilisation des spectres en
précédent: Utilisation des spectres en
Table des matières
Index
Brun Luc
2004-03-25
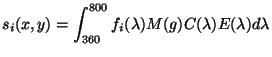
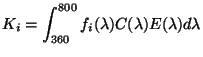
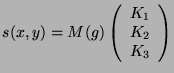
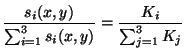
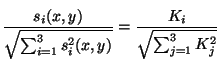
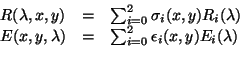
![]() associé au pixel de
coordonnées
associé au pixel de
coordonnées ![]() est donnée par une équation similaire à
l'équation 2.21:
est donnée par une équation similaire à
l'équation 2.21: