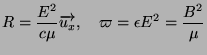Une onde électromagnétique est définie par deux champs ![]() , et
, et
![]() fonctions de 4 variables (trois coordonnées spaciales et une
temporelle). Une onde électromagnétique est qualifiée de plane
lorsque ses coordonnées spaciales ne dépendent que d'un seul
paramètre. On obtient alors deux champs
fonctions de 4 variables (trois coordonnées spaciales et une
temporelle). Une onde électromagnétique est qualifiée de plane
lorsque ses coordonnées spaciales ne dépendent que d'un seul
paramètre. On obtient alors deux champs ![]() et
et ![]() fonction
d'une coordonnée spaciale et d'une coordonnée temporelle (voir
Figure 2.3).
fonction
d'une coordonnée spaciale et d'une coordonnée temporelle (voir
Figure 2.3).
ondes_planesIllustration d'une onde électromagnétique
plane. L'onde se propage dans ce cas sur l'axe des ![]()
Si une onde électromagnétique se propage dans un milieu dépourvu de
charges et de courant (![]() et
et ![]() ), les équations de Maxwell se
simplifient et permettent d'obtenir deux équations differentielles décrivant l'évolution des champs
), les équations de Maxwell se
simplifient et permettent d'obtenir deux équations differentielles décrivant l'évolution des champs ![]() et
et ![]() :
:
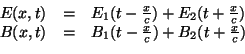
Si
![]() définit le vecteur unitaire de propagation de l'onde plane,
les équations de Maxwell nous permettent encore une fois de lier les
champs
définit le vecteur unitaire de propagation de l'onde plane,
les équations de Maxwell nous permettent encore une fois de lier les
champs ![]() et
et ![]() :
: