




suivant: Mise en oeuvre
monter: Opérateurs différentiels
précédent: Passage au discret
Table des matières
Index
Canny [Can86] modélise un contour 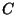 comme la superposition
d'un saut d'amplitude
comme la superposition
d'un saut d'amplitude 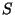 et d'un bruit blanc
et d'un bruit blanc 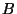 .
.
La fonction 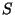 est modélisée par la fonction
est modélisée par la fonction
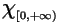 où
où 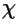 est la fonction caractéristique.
est la fonction caractéristique.
Suivant ce formalisme, le détecteur de contour idéal 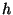 est celui
qui, convolué à
est celui
qui, convolué à 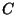 , présente un maximum en 0. Cette contrainte
n'étant pas suffisante pour déterminer
, présente un maximum en 0. Cette contrainte
n'étant pas suffisante pour déterminer 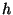 , Canny impose trois
conditions supplémentaires à son détecteur de contour :
, Canny impose trois
conditions supplémentaires à son détecteur de contour :
- Une bonne détection
- Une bonne localisation
- Une faible multiplicité des maxima dûs au bruit.
La formalisation de ces trois conditions impose à la fonction 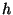 de
respecter l'équation différentielle suivante :
Les conditions aux limites imposées à la fonction
de
respecter l'équation différentielle suivante :
Les conditions aux limites imposées à la fonction 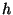 permettent
de fixer les paramètres
permettent
de fixer les paramètres
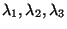 . Les
conditions imposées par Canny permettent d'obtenir une fonction
à support fini
. Les
conditions imposées par Canny permettent d'obtenir une fonction
à support fini ![$ [-M,M]$](img810.png) :
Malheureusement, ces conditions donnent une fonction
:
Malheureusement, ces conditions donnent une fonction 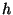 très
coûteuse à implémenter. Partant de ce constat,
Deriche [Der87] a défini d'autres conditions aux limites
donnant à la fonction
très
coûteuse à implémenter. Partant de ce constat,
Deriche [Der87] a défini d'autres conditions aux limites
donnant à la fonction 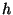 un support infini :
Ces conditions initiales donnent la fonction :
L'analyse des critères donnés par Canny [Can86] montre
que les meilleures performances du filtre sont obtenues pour
un support infini :
Ces conditions initiales donnent la fonction :
L'analyse des critères donnés par Canny [Can86] montre
que les meilleures performances du filtre sont obtenues pour 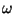 tendant vers 0. On obtient à ce moment là
tendant vers 0. On obtient à ce moment là
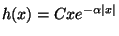 avec
avec
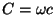 . Le paramètre
. Le paramètre 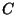 est un paramètre de
normalisation, le paramètre
est un paramètre de
normalisation, le paramètre 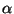 contrôle quant à lui la
sensibilité de l'opérateur de détection de contour. Une
augmentation de
contrôle quant à lui la
sensibilité de l'opérateur de détection de contour. Une
augmentation de 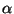 favorise la détection au détriment de la
localisation et vice-versa. Le paramètre
favorise la détection au détriment de la
localisation et vice-versa. Le paramètre 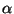 joue ici
exactement le même rôle que le paramètre
joue ici
exactement le même rôle que le paramètre 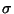 dans la
définition du gradient de la gaussienne.
dans la
définition du gradient de la gaussienne.
Deriche construit à partir de 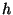 une fonction de lissage 1D
une fonction de lissage 1D 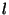 définie par :
définie par :
On définit alors la fonction de lissage 2D 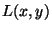 par :
La fonction
par :
La fonction 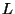 joue ici le rôle de la gaussienne, et le filtrage
de l'image s'obtient en convoluant celle-ci avec
joue ici le rôle de la gaussienne, et le filtrage
de l'image s'obtient en convoluant celle-ci avec 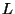 . Une fois l'image
lissée, on peut calculer son gradient ou son laplacien. Ces deux
opérations s'effectuent en convoluant l'image avec le gradient ou le
laplacien de
. Une fois l'image
lissée, on peut calculer son gradient ou son laplacien. Ces deux
opérations s'effectuent en convoluant l'image avec le gradient ou le
laplacien de 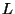 .
.
L'avantage des opérateurs de Deriche par rapport à ceux de Canny
vient du fait que les techniques de la transformée en
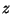 [Der87], appliquées à la fonction
[Der87], appliquées à la fonction 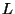 et à ses
dérivées, permettent de calculer de façon récursive la
convolution des opérateurs de Deriche avec l'image. Si, par exemple,
nous effectuons la convolution d'un signal mono-dimensionnel
et à ses
dérivées, permettent de calculer de façon récursive la
convolution des opérateurs de Deriche avec l'image. Si, par exemple,
nous effectuons la convolution d'un signal mono-dimensionnel 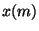 avec la fonction échantillonnée
avec la fonction échantillonnée 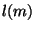 , le signal final
, le signal final 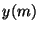 se
déduit des équations suivantes [DC87] :
se
déduit des équations suivantes [DC87] :
où 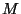 représente la taille du signal et où les coefficients
représente la taille du signal et où les coefficients
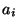 et
et 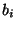 se déduisent du paramètre
se déduisent du paramètre 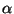 .
.
L'application de l'algorithme décrit par les
équations précédentes nécessite 8 opérations par point
quelle que soit la valeur de 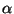 . Les filtres de Deriche
présentent donc les avantages suivants :
. Les filtres de Deriche
présentent donc les avantages suivants :
- Ils s'appuient sur une étude théorique permettant de juger et comparer différents détecteurs de contours
- Leur expression, plus simple que la gaussienne, permet, grâce à
la transformée en
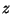 , d'obtenir une définition récursive de la
convolution. Cette récursivité permet d'effectuer l'opération de
convolution en un nombre fixe d'opérations par point de l'image,
indépendamment du paramètre
, d'obtenir une définition récursive de la
convolution. Cette récursivité permet d'effectuer l'opération de
convolution en un nombre fixe d'opérations par point de l'image,
indépendamment du paramètre 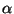 .
.
Shen et Castan [SC92,CZS89] ont adopté une démarche
similaire à celle de Canny [Can86]. Les différences entre
les deux méthodes portent sur la formalisation des critères
décrivant un détecteur de contour optimal. La fonction obtenue par
Shen est égale à
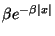 . Cette fonction permet de
définir des opérateurs de lissage, de gradient et de laplacien et
d'effectuer une transformée en
. Cette fonction permet de
définir des opérateurs de lissage, de gradient et de laplacien et
d'effectuer une transformée en 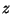 [Mon90] permettant une
implémentation récursive.
[Mon90] permettant une
implémentation récursive.





suivant: Mise en oeuvre
monter: Opérateurs différentiels
précédent: Passage au discret
Table des matières
Index
Brun Luc
2004-03-25
![]() comme la superposition
d'un saut d'amplitude
comme la superposition
d'un saut d'amplitude ![]() et d'un bruit blanc
et d'un bruit blanc ![]() .
.
![]() est celui
qui, convolué à
est celui
qui, convolué à ![]() , présente un maximum en 0. Cette contrainte
n'étant pas suffisante pour déterminer
, présente un maximum en 0. Cette contrainte
n'étant pas suffisante pour déterminer ![]() , Canny impose trois
conditions supplémentaires à son détecteur de contour :
, Canny impose trois
conditions supplémentaires à son détecteur de contour :

![]() une fonction de lissage 1D
une fonction de lissage 1D ![]() définie par :
définie par :
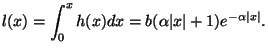
![]() [Der87], appliquées à la fonction
[Der87], appliquées à la fonction ![]() et à ses
dérivées, permettent de calculer de façon récursive la
convolution des opérateurs de Deriche avec l'image. Si, par exemple,
nous effectuons la convolution d'un signal mono-dimensionnel
et à ses
dérivées, permettent de calculer de façon récursive la
convolution des opérateurs de Deriche avec l'image. Si, par exemple,
nous effectuons la convolution d'un signal mono-dimensionnel ![]() avec la fonction échantillonnée
avec la fonction échantillonnée ![]() , le signal final
, le signal final ![]() se
déduit des équations suivantes [DC87] :
se
déduit des équations suivantes [DC87] :
![]() . Les filtres de Deriche
présentent donc les avantages suivants :
. Les filtres de Deriche
présentent donc les avantages suivants :
![]() . Cette fonction permet de
définir des opérateurs de lissage, de gradient et de laplacien et
d'effectuer une transformée en
. Cette fonction permet de
définir des opérateurs de lissage, de gradient et de laplacien et
d'effectuer une transformée en ![]() [Mon90] permettant une
implémentation récursive.
[Mon90] permettant une
implémentation récursive.