




suivant: Les opérateurs de convolution
monter: Traitements d'images couleur
précédent: Traitements d'images couleur
Table des matières
Index
Opérateurs différentiels
Ces méthodes considèrent généralement l'image comme la
discrétisation d'un signal continu 2D. On a donc :
où 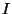 est l'image discrète,
est l'image discrète, 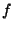 le signal continu, et
le signal continu, et 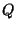 un
opérateur d'échantillonnage. La recherche de contours dans
un
opérateur d'échantillonnage. La recherche de contours dans 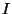 (donc de sauts de valeurs) se caractérise dans
(donc de sauts de valeurs) se caractérise dans 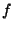 par des maxima de
la dérivé. On introduit donc l'opérateur différentiel
par des maxima de
la dérivé. On introduit donc l'opérateur différentiel
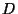 . Nous verrons dans la section 6.1.5 comment
l'information couleur peut être traitée par ce type d'approche. La
plupart des méthodes de détection de contours étant plus
spécifiquement dédiées au traitement d'images
mono-dimensionnelles, nous allons dans cette section nous limiter à
ce cas. Nous supposerons de plus que
. Nous verrons dans la section 6.1.5 comment
l'information couleur peut être traitée par ce type d'approche. La
plupart des méthodes de détection de contours étant plus
spécifiquement dédiées au traitement d'images
mono-dimensionnelles, nous allons dans cette section nous limiter à
ce cas. Nous supposerons de plus que 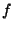 appartient à
appartient à
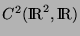 , l'ensemble des fonctions continuement deux fois
différentiables de dans . L'ensemble des fonctions
susceptibles de donner une même discrétisation
, l'ensemble des fonctions continuement deux fois
différentiables de dans . L'ensemble des fonctions
susceptibles de donner une même discrétisation 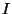 étant
important, cette dernière condition n'est pas très restrictive.
étant
important, cette dernière condition n'est pas très restrictive.
La différentielle de 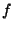 peut donc s'exprimer de la façon suivante :
peut donc s'exprimer de la façon suivante :
 |
(6.1) |
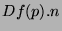 est donc la dérivée de
est donc la dérivée de 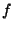 dans la direction
dans la direction 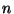 (comme
seule la direction de n nous intéresse, on peut prendre
(comme
seule la direction de n nous intéresse, on peut prendre 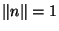 ). Si nous introduisons l'opérateur gradient
défini par :
l'équation 6.1 s'écrit :
). Si nous introduisons l'opérateur gradient
défini par :
l'équation 6.1 s'écrit :
 |
(6.2) |
où 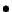 désigne le produit scalaire.
désigne le produit scalaire.
On a, de plus, par l'équation 6.2 :
Donc, en tout point la norme du gradient permet de connaître la
variation maximum de la différentielle. De plus, le maximum étant
atteint pour 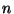 colinéaire à
colinéaire à
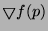 , la direction du
gradient donne la direction de plus grande variation de la fonction
, la direction du
gradient donne la direction de plus grande variation de la fonction
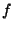 .
.
Les directions de variation de 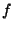 correspondant à des maxima de la
différentielle de
correspondant à des maxima de la
différentielle de 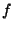 , on peut également chercher ces directions
par les zéros de la différentielle seconde de
, on peut également chercher ces directions
par les zéros de la différentielle seconde de 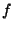 . Si
. Si 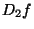 désigne cette différentielle seconde, on a :
désigne cette différentielle seconde, on a :
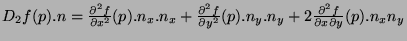 |
(6.3) |
La fonction 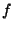 présentera une variation locale suivant une
direction
présentera une variation locale suivant une
direction 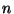 , si à
, si à 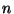 fixé la fonction
fixé la fonction 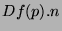 présente un
maximum local. Ce maximum local se traduira, toujours à
présente un
maximum local. Ce maximum local se traduira, toujours à 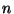 fixé,
par un zéro de la fonction
fixé,
par un zéro de la fonction 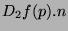 en ce point.
en ce point.
Afin d'alléger les calculs, on cherche les zéros du laplacien
plutôt que les zéros de la différentielle seconde. Le laplacien
de la fonction 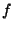 , noté f, est défini par :
, noté f, est défini par :
Le laplacien étant invariant par rotation, le calcul des zéros du
laplacien ne fait pas intervenir la direction 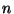 de plus grande
variation de
de plus grande
variation de 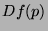 . L'utilisation du laplacien évite donc de
calculer le gradient en plus de la différentielle seconde.
. L'utilisation du laplacien évite donc de
calculer le gradient en plus de la différentielle seconde.
Les zéros du laplacien ne correspondent généralement pas aux
zéros de 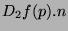 , toutefois Marr [MH80] a montré qu'il
y avait coïncidence entre les zéros des deux fonctions au point
, toutefois Marr [MH80] a montré qu'il
y avait coïncidence entre les zéros des deux fonctions au point
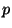 si les variations d'intensité étaient linéaires sur la ligne
de passage par zéro et sur les lignes parallèles dans un voisinage
de
si les variations d'intensité étaient linéaires sur la ligne
de passage par zéro et sur les lignes parallèles dans un voisinage
de 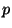 . Le laplacien peut donc être vu comme une bonne approximation
de la différentielle seconde.
. Le laplacien peut donc être vu comme une bonne approximation
de la différentielle seconde.
Sous-sections





suivant: Les opérateurs de convolution
monter: Traitements d'images couleur
précédent: Traitements d'images couleur
Table des matières
Index
Brun Luc
2004-03-25
![]() peut donc s'exprimer de la façon suivante :
peut donc s'exprimer de la façon suivante :
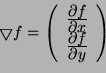
![]() correspondant à des maxima de la
différentielle de
correspondant à des maxima de la
différentielle de ![]() , on peut également chercher ces directions
par les zéros de la différentielle seconde de
, on peut également chercher ces directions
par les zéros de la différentielle seconde de ![]() . Si
. Si ![]() désigne cette différentielle seconde, on a :
désigne cette différentielle seconde, on a :
![]() , noté f, est défini par :
, noté f, est défini par :
![]() , toutefois Marr [MH80] a montré qu'il
y avait coïncidence entre les zéros des deux fonctions au point
, toutefois Marr [MH80] a montré qu'il
y avait coïncidence entre les zéros des deux fonctions au point
![]() si les variations d'intensité étaient linéaires sur la ligne
de passage par zéro et sur les lignes parallèles dans un voisinage
de
si les variations d'intensité étaient linéaires sur la ligne
de passage par zéro et sur les lignes parallèles dans un voisinage
de ![]() . Le laplacien peut donc être vu comme une bonne approximation
de la différentielle seconde.
. Le laplacien peut donc être vu comme une bonne approximation
de la différentielle seconde.