Contrairement au modèle de Beckmann-Spizzichino [BS87] (Section 2.2.2), le modèle de Torrance-Sparrow est basé sur l'optique géométrique. Ce modèle néglige donc l'aspect électromagnétique de la lumière. Cette approximation n'est valide que si les irrégularités de la surface sont bien supérieures à la longueur d'onde de la source.
Le modèle de surface utilisé par Torrance-Sparrow est basé sur une
modélisation des irrégularités par une série de micro-facettes. Chaque
facette est décrite par l'angle ![]() entre sa normale et la normale à
la surface macroscopique (Figure 2.9). Si nous
supposons la surface isotropique, la distribution des normales de
facettes est rotationnellement symétrique par rapport à
entre sa normale et la normale à
la surface macroscopique (Figure 2.9). Si nous
supposons la surface isotropique, la distribution des normales de
facettes est rotationnellement symétrique par rapport à ![]() . La
distribution de
. La
distribution de ![]() peut alors être modélisée par une fonction
unidimensionnelle telle qu'une distribution normale de moyenne nulle
et d'écart-type
peut alors être modélisée par une fonction
unidimensionnelle telle qu'une distribution normale de moyenne nulle
et d'écart-type
![]() . Sachant que
. Sachant que ![]() ne peut varier qu'entre 0 et
ne peut varier qu'entre 0 et
![]() , la fonction de densité de probabilité de
, la fonction de densité de probabilité de ![]() est égale
à :
est égale
à :
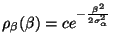 avec
avec 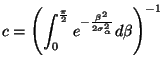
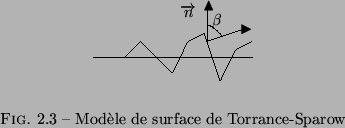
Ce modèle de surface et les lois de l'optique géométrique permettent d'obtenir une expression explicite de l'irradiance incidente à un capteur de la caméra générée par un patch de surface :
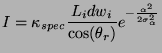
Le terme
![]() a approximativement la même
signification que le terme
a approximativement la même
signification que le terme
![]() dans le modèle
de Beckmann-Spizzichino (Section 2.2.2) et correspond
à un lobe spéculaire. La modélisation de la réflexion de
Torrance-Sparrow en utilisant des micro-facettes et les lois de
l'optique géométrique conduisent donc à un modèle ne présentant qu'un
lobe spéculaire. Ce résultat est attendu dans la mesure ou les lois
de l'optique géométriques ne sont valides que pour des surfaces
rugueuses. Or le pic spéculaire de Beckmann-Spizzichino n'apparaît que
pour des surfaces lisses ou modérément rugueuses
(Section 2.2.2).
dans le modèle
de Beckmann-Spizzichino (Section 2.2.2) et correspond
à un lobe spéculaire. La modélisation de la réflexion de
Torrance-Sparrow en utilisant des micro-facettes et les lois de
l'optique géométrique conduisent donc à un modèle ne présentant qu'un
lobe spéculaire. Ce résultat est attendu dans la mesure ou les lois
de l'optique géométriques ne sont valides que pour des surfaces
rugueuses. Or le pic spéculaire de Beckmann-Spizzichino n'apparaît que
pour des surfaces lisses ou modérément rugueuses
(Section 2.2.2).
Torrance et Sparrow ajoutent un terme Lambertien à leur équation de réflexion qui devient :
L'utilisation de l'optique géométrique conduit à des formules moins complexes que celles induites par les lois de l'électromagnétique. Torrance et Sparrow sont donc conduits à faire moins d'hypothèses simplificatrices que Beckmann et Spizzichino. Leur modèle inclue notamment le coefficient de Fresnel et un coefficient de masquage. Ce modèle est donc applicable à des objets non conducteurs et permet de tenir compte du masquage entre différents éléments de la scène. Ce modèle a toutefois un certain nombre de limitations :