Le modèle de Nayar [NIK91] peut se concevoir comme une
synthèse des modèles de Beckmann-Spizzichino et Torrance-Sparrow
(Sections 2.2.2 et 2.2.3). Plusieurs
expériences menées par Nayar montrent que le coefficient de Fresnel
![]() et le facteur d'atténuation
et le facteur d'atténuation ![]() du modèle de Torrance-Sparrow
(équation 2.10) restent approximativement constants en
fonction de
du modèle de Torrance-Sparrow
(équation 2.10) restent approximativement constants en
fonction de ![]() et
et ![]() . Le coefficient
. Le coefficient
![]() peut donc être
considéré comme constant. De plus si l'on se place dans un protocole
expérimental où la source est variable tandis que la direction
d'observation reste constante, les angles
peut donc être
considéré comme constant. De plus si l'on se place dans un protocole
expérimental où la source est variable tandis que la direction
d'observation reste constante, les angles ![]() et
et ![]() peuvent être
considérés comme constants. Sous ces conditions, l'irradiance du lobe
spéculaire peut s'exprimer par :
peuvent être
considérés comme constants. Sous ces conditions, l'irradiance du lobe
spéculaire peut s'exprimer par :
En revanche si l'on considère des variations simultanées de la source
lumineuse et de l'observateur nous ne pouvons négliger le terme
![]() dans le modèle de Torrance-Sparrow
(équation 2.10). L'expression du lobe spéculaire
devient alors :
dans le modèle de Torrance-Sparrow
(équation 2.10). L'expression du lobe spéculaire
devient alors :
Notons que l'équation 2.13 devra être utilisée si
l'on considère simultanément plusieurs pixels et donc plusieurs
normales avec des angles
![]() et
et ![]() différents. L'équation 2.12 sera en revanche utilisée
lorsque l'on considérera un même pixel soumis à différents
illuminants. Dans ce dernier cas
différents. L'équation 2.12 sera en revanche utilisée
lorsque l'on considérera un même pixel soumis à différents
illuminants. Dans ce dernier cas ![]() et
et ![]() sont variables tandis
que
sont variables tandis
que ![]() et
et ![]() peuvent être considérés comme des constantes.
peuvent être considérés comme des constantes.
Le pic spéculaire du modèle de Beckmann-Spizzichino peut être
approximé par une fonction ![]() valant
valant ![]() dans la direction spéculaire
et 0 partout ailleurs. L'intensité du pic spéculaire est alors égale
à :
dans la direction spéculaire
et 0 partout ailleurs. L'intensité du pic spéculaire est alors égale
à :
Finalement, le lobe diffus correspondant à la réflexion Lambertienne peut être ajouté au modèle de façon à avoir une intensité de pixel liée à la géométrie de la scène par :
Notez encore une fois que le cas d'un observateur variable (équation 2.15) peut s'appliquer soit :
Nayar a de plus établi des ponts entre les deux
modèles en remarquant que puisque ![]() est l'angle entre
est l'angle entre
![]() et
la normale nous avons (équation 2.6) :
et
la normale nous avons (équation 2.6) :
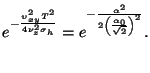
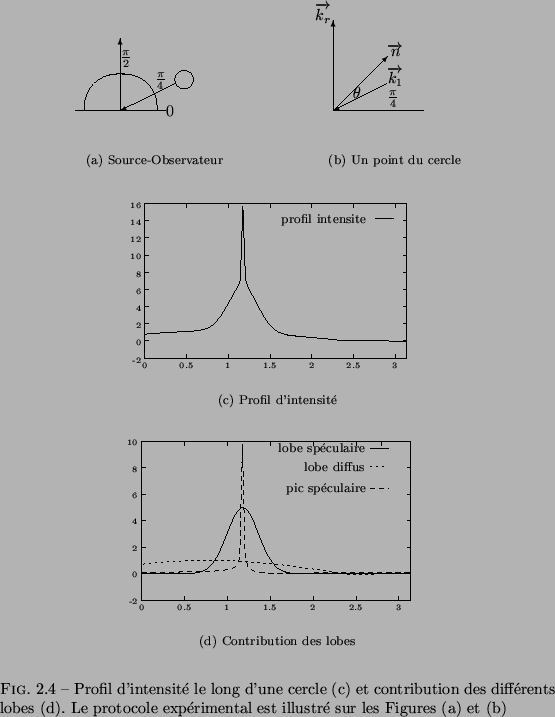
La Figure 2.10 illustre le modèle de Nayar sur
un cercle de rayon 1 éclairé par une source lumineuse placée en
![]() et observé en
et observé en
![]() (Figure 2.10(a)). Le modèle utilisé est
l'équation 2.15. Un point du cercle faisant un
angle
(Figure 2.10(a)). Le modèle utilisé est
l'équation 2.15. Un point du cercle faisant un
angle ![]() avec l'horizontale vérifiera
(Figure 2.10(b)):
avec l'horizontale vérifiera
(Figure 2.10(b)):
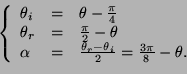
La direction spéculaire
![]() se situe donc en
se situe donc en
![]() .
.
L'intensité le long du cercle en fonction de l'angle ![]() est
représentée sur la figure 2.10(c). La
contribution de chacune des composante est quand à elle illustrée sur
la Figure 2.10(d). Les constantes choisies pour
cette figure sont
est
représentée sur la figure 2.10(c). La
contribution de chacune des composante est quand à elle illustrée sur
la Figure 2.10(d). Les constantes choisies pour
cette figure sont
![]() et
et
![]() .
.