Différents modèles de réflexion

Les mécanisme d'absorption -réflexion d'une onde électromagnétisme peuvent s'expliquer par les lois de la mécanique classique (celle des ondes électromagnétiques) ou les lois de la mécanique quantique. Attardons nous un instant sur cette dernière approche qui permet de donner une bonne intuition du phénomène. Une onde électromagnétique de longueur d'onde $\lambda$ peut d'un point de vue quantique, se voir comme la propagation d'un ensemble de photons d'énergie $h\frac{c}{\lambda}=h\nu$, où $h$ est la constante de plank. Lorsqu'un photon heurte un électron il y transmet son énergie et l'électron passe d'un état au repos à un état excité. L'ensemble des électrons susceptible de changer d'état et la quantité d'énergie que peut absorber chaque électron dans un milieu donné caractérise les longueurs d'ondes du champ électromagnétique incident qui seront absorbées et donc la couleur du milieu.

Le calcul exact du spectre réfléchi requiert donc une connaissance extrêmement précise des caractéristiques du milieu qui est rarement disponible. De plus comme nous l'avons rapidement abordé dans le paragraphe précédent le spectre réfléchie dépend de la géométrie de l'objet qui est souvent connue que d'un point de vue macroscopique quand elle n'est pas totalement inconnue (le plan infini est une abstraction mathématique).

Du fait de ces limitations de nombreux modèles ont été établis afin de rendre compte ne fusse que de façon approximative (voir empirique) des phénomènes de réfraction - absorption.

Il est relativement clair que de nombreux matériaux réfléchissent la lumière de façon très différente. Un pot de céramique et de cuivre auront par exemple des propriétés optiques très différentes. Ces différents types de réflexions seront donc caractérisés par différents modèles décrivant différent types de matériaux. On distingue notamment [Sha85,Hea89,Hun75] :

1. Les matériaux conducteurs comme les métaux. Comme nous le verrons par la suite ces matériaux atténuent rapidement l'onde incidente si bien que le phénomène de réflexion est essentiellement un phénomène de surface.

2. Les matériaux peu conducteurs également appelés diélectriques tels que le verre. Ces matériaux laissent au contraire pénétrer profondément l'onde incidente dans l'objet. La description de la réflexion exige donc pour ces matériaux une modélisation des phénomènes optiques dans le matériau.

3. Les matériaux optiquement homogènes. Ces matériaux ont un indice de réfraction constant à l'intérieur du matériau. Pour ce type d'objet la réflexion de l'onde incidente peut être décrite uniquement à partir de la réflexion de l'onde sur la surface du matériau. Les métaux, le verre, les cristaux sont des exemples communs de matériaux homogènes.

4. Les matériaux optiquement in-homogènes sont composés d'un matériau qui inclue de nombreuses particules colorantes dont les propriétés optiques sont différentes de celles du support. Dans ce cas, le calcul de l'onde réfléchie doit tenir compte de l'interaction de l'onde incidente avec les particules de colorant. Les plastiques, le papier, les textiles et les peintures font partie des matériaux optiquement in-homogènes.

Notez que les points 1 et 2 indiquent si le phénomène de réflexion est un phénomène de surface. Les points 3 et 4 décomposent les matériaux en fonction des phénomènes optiques se produisant à l'intérieur de ceux ci.

Un autre paramètre important d'une surface est sa rugosité. Ainsi, des matériaux homogènes et parfaitement lisses réfléchissent la lumière dans une direction symétrique au rayon incident par rapport à la normale. Ce phénomène est appelé une réflexion spéculaire. Inversement des matériaux homogènes plus rugueux diffusent la lumière autour de la réflexion spéculaire. L'ensemble des rayons réfléchis est appelé le lobe spéculaire.

L'électromagnétisme permet de décrire les propriétés optiques d'un matériau à l'aide des constantes $\mu$, $\epsilon$ et $\sigma$ décrivant respectivement la perméabilité magnétique, la permittivité électrique et la conductivité du matériau (Table 2.1). Les propriétés optiques d'un matériau peuvent également être résumées à l'aide d'une seule variable appelée l'indice complexe de réfraction et noté $M=n-iK_0$ où $n$ et $K_0$ sont deux réels. La constante $n$ est appelée la part réfractive de $M$. Dans des matériaux n'atténuant pas le signal ($K_0=0$), la constante $n$ est égale au rapport entre la vitesse de la lumière dans le vide et dans le matériau. La constante $K_0$ est directement impliquée dans l'atténuation de l'onde électromagnétique dans le matériau. En effet l'irradiance d'une onde planaire de fréquence $\omega$ de direction $x>0$ qui heurte le plan $(Ozy)$ est égale à :

$$I(x) = I(0)e^{-\disp \frac{2\omega K_0x}{c}}$$

où $c$ est la vitesse de la lumière dans le vide.

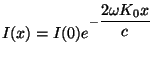
Cette atténuation de l'énergie de l'onde incidente ce fait au bénéfice de l'apparition d'un courant appelé courant de surface. La profondeur $x=\frac{c}{2\omega K_0}$ est appelé la profondeur de peau du matériau. Les constantes $n$ et $K_0$ peuvent être calculée en fonction de $\mu,\epsilon$ et $\sigma$ en utilisant les lois de Maxwell [SH81] :

$$\begin{array}{lll} n(\lambda)&=& \frac{\mu\epsilon c^2}{2}\le... ...{\lambda\sigma}{2\pi c\epsilon}\right)^2}\right].\\ \end{array}$$ (2.2)

Nous pouvons immédiatement observer que $n$ et $K_0$ (et donc $M$) ne dépendent que de la longueur d'onde de l'onde incidente. De plus pour des matériaux conducteurs $\sigma$ sera important et donc $K_0$ également. L'onde électromagnétique pénètre donc faiblement dans les matériaux conducteurs pour lesquels le phénomène de la réflexion est essentiellement un phénomène lié à la surface du matériau. Inversement, des matériaux peu conducteurs auront un $K_0$ faible ce qui favorisera la pénétration de l'onde dans le matériau. Ce phénomène devra donc être pris en compte dans la modélisation de la réflexion.

Un dernier paramètre fondamental dans la description de la réflexion d'une onde électromagnétique est le Coefficient de Fresnel qui décrit la fraction de l'onde incidente réfléchie par la surface d'un matériau. Dans le cas d'un matériau isotropique et homogène, la réflexion d'une onde non polarisée heurtant une surface lisse avec un angle $\theta_l$ produit un coefficient de Fresnel égal à :

$$F(\theta_l,\lambda)=\frac{1}{2}\left(R_{\Vert}(\theta_l,\lambda)+R_{\bot}(\theta_l,\lambda)\right)$$

où $R_{\Vert}(\theta_l,\lambda)$ et $R_{\bot}(\theta_l,\lambda)$ décrivent le coefficient de Fresnel dans le cas d'une onde polarisée respectivement parallèlement et perpendiculairement au plan d'incidence (plan contenant la normale à la surface et le rayon incident).

Les termes $R_{\Vert}(\theta_l,\lambda)$ et $R_{\bot}(\theta_l,\lambda)$ peuvent se déduire de la théorie des ondes électromagnétiques. Toutefois la forme explicite de ces termes n'étant pas utile pour la suite de ce document nous nous contenterons de noter que $R_{\Vert}(\theta_l,\lambda)$ et $R_{\bot}(\theta_l,\lambda)$ peuvent s'exprimer sous forme d'une fraction de termes dépendant de $\theta_l$, $n(\lambda)$ et $K_0(\lambda)$.