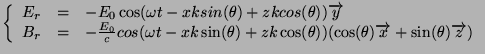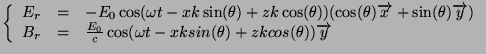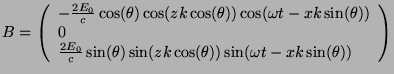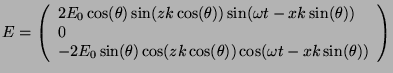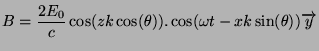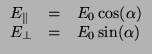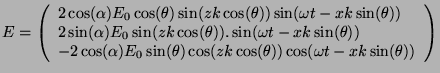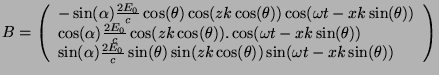suivant: Différents modèles de réflexion
monter: Les ondes électromagnétiques
précédent: Onde planes mono-chromatiques
Table des matières
Index
Réflection d'une onde plane monochromatique sur un métal parfait
Soit une surface 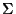 de densité surfacique de courant
de densité surfacique de courant 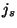 et
de densité surfacique de charge
et
de densité surfacique de charge 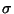 séparant deux milieux 1 et
2. Un champ électromagnétique heurtant la surface peut être
décomposé en ces composantes tangencielles
séparant deux milieux 1 et
2. Un champ électromagnétique heurtant la surface peut être
décomposé en ces composantes tangencielles 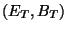 et normales
et normales
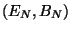 à la surface. Le lien entre le champ de part et d'autre de
la surface est donné par les équations suivantes:
à la surface. Le lien entre le champ de part et d'autre de
la surface est donné par les équations suivantes:
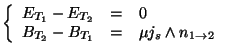 et et 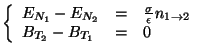 |
(2.1) |
On observe donc une continuité de la composante tangencielle du champ
électrique et de la composante normale du champ magnétique lors du
passage entre les deux milieux. En revanche, la composante normale du
champ électrique et tangencielle du champ magnétique sont
discontinues. Le champ magnétique est continue uniquement dans le cas
d'une densité de charge 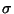 et d'une densité de courant
et d'une densité de courant 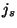 nulles.
nulles.
Un métal parfait est un métal de conductivité
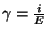 infinie. Aucune source de champ magnétique, et donc aucun champ ne
peut exister à l'intérieur de ce métal. On a donc:
infinie. Aucune source de champ magnétique, et donc aucun champ ne
peut exister à l'intérieur de ce métal. On a donc:
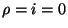
et
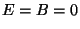
Lorqu'un champ magnétique rencontre une surface plane d'un tel
métal, le champ magnétique incident à la surface du métal est égal au
champ magnétique incident plus le champ magnétique réfléchi. Aucun
champ ne pouvant exister à l'intérieur du métal, on obtient par les
équations 2.1:
en supposant que le plan 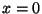 définit la surface de séparation entre
le métal et le vide et que les vecteurs
définit la surface de séparation entre
le métal et le vide et que les vecteurs 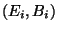 soient inclus dans
le plan
soient inclus dans
le plan 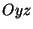 . Notez que les champs électriques incident et réfléchi
s'annulant à tout instant à la surface du métal doivent avoir la
même fréquence, donc la réflexion sur un métal parfait ne change pas
la couleur de la lumière incidente.
. Notez que les champs électriques incident et réfléchi
s'annulant à tout instant à la surface du métal doivent avoir la
même fréquence, donc la réflexion sur un métal parfait ne change pas
la couleur de la lumière incidente.
Soient
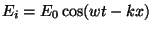 et
et
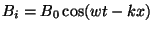 les champs
électriques et magnétiques d'une onde plane monochromatique. Le champ
magnétique réfléchis est donné par
les champs
électriques et magnétiques d'une onde plane monochromatique. Le champ
magnétique réfléchis est donné par
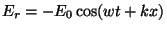 et
et
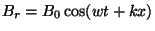 . L'onde résultante en tout point est donc égale
à:
. L'onde résultante en tout point est donc égale
à:
Les composantes spaciales et temporelles des champs magnétiques et
électriques sont décorrelées. On dit dans ce cas que l'onde est
stationnaire (voir Figure 2.4).
Le vecteur de Poynting de l'onde résultante est égal à :
La densité volumique d'énergie est donnée par :
La moyenne temporelle de cette onde est indépendante de la coordonnée
spaciale x :
ondes_reflechiesTracé des deux fonctions
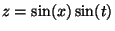 (a) et
(a) et
 (b). Ces deux tracés ne représentent
pas à proprement parler des l'amplitude d'une onde élecromagnétique,
mais nous renseigne sur l'allure de cette amplitude dans le cas d'une
onde stationnnaire (a) et non stationnaire (b)
(b). Ces deux tracés ne représentent
pas à proprement parler des l'amplitude d'une onde élecromagnétique,
mais nous renseigne sur l'allure de cette amplitude dans le cas d'une
onde stationnnaire (a) et non stationnaire (b)
Etant donnés une onde électromagnétique 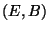 et un plan d'incidence défini
par
et un plan d'incidence défini
par 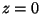 , l'on dira que:
, l'on dira que:
Cette notion de polarisation peut sembler un peut abstraite pour un
être humain qui ne percoit pas la polarisation de la lumière. Elle est
toutefois très concrète pour une grande quantité d'insectes qui sont
sensibles à cette propriété. On peut notamment montrer que les
différentes parties du ciel sont polarisées différement celon l'heure
de la journée (et donc la position du soleil). Cette propriété permet
à de nombreux insectes de s'orienter même par ciel couvert. On peut
également montrer que de nombreuses ailes de papillons polarisent la
lumière. Cette propriété permet notamment aux papillons de ce
différencier entre sexes et entre espèces voisines lors de la
reproduction.
Soit une onde électromagnétique plane d'équation
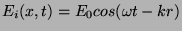 heurtant une surface
heurtant une surface 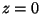 avec un angle d'incidence
avec un angle d'incidence 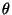 . La
partie
. La
partie 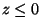 étant occupée par un métal parfait, on peut
montrer [Lum95] que l'onde réfléchie a pour équation :
étant occupée par un métal parfait, on peut
montrer [Lum95] que l'onde réfléchie a pour équation :
- Si l'onde électromagnétique est polarisée perpendiculairement:
- Si l'onde électromagnétique est polarisée parallèlement:
Si nous ajoutons l'onde incidente à l'onde réfléchie, nous obtenons:
- Dans le cas perpendiculaire:
et:
- Dans le cas parallèle:
et
Dans le cas général, où l'onde n'est polarisée ni
perpendiculairement ni parallèlement, le vecteur 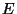 peut être
décomposé en deux composantes polarisées perpendiculairement et
parallelement:
Ce qui nous donne les ondes réfléchies:
et
Ces dernières formules appellent plusieurs remarques:
peut être
décomposé en deux composantes polarisées perpendiculairement et
parallelement:
Ce qui nous donne les ondes réfléchies:
et
Ces dernières formules appellent plusieurs remarques:
- La fréquence du signal réfléchie n'est pas modifié (on reste en
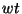 ).
).
- Le facteur d'atténuation du signal réfléchie ne dépend pas de la fréquence de l'onde incidente.
Donc le métal parfait renvera la même quantitée d'énergie quelque
soit la longueur d'onde de la lumière incidente. Celui ci se comporte
donc comme un mirroir et n'est utile qu' en tant que modèle lorsque
l'on veut modéliser les caractéristiques optiques des matériaux. Nous
allons à présent étudier des modèles un peu plus réaliste.





suivant: Différents modèles de réflexion
monter: Les ondes électromagnétiques
précédent: Onde planes mono-chromatiques
Table des matières
Index
Brun Luc
2004-03-25
![]() de densité surfacique de courant
de densité surfacique de courant ![]() et
de densité surfacique de charge
et
de densité surfacique de charge ![]() séparant deux milieux 1 et
2. Un champ électromagnétique heurtant la surface peut être
décomposé en ces composantes tangencielles
séparant deux milieux 1 et
2. Un champ électromagnétique heurtant la surface peut être
décomposé en ces composantes tangencielles ![]() et normales
et normales
![]() à la surface. Le lien entre le champ de part et d'autre de
la surface est donné par les équations suivantes:
à la surface. Le lien entre le champ de part et d'autre de
la surface est donné par les équations suivantes:
![]() et d'une densité de courant
et d'une densité de courant ![]() nulles.
nulles.
![]() infinie. Aucune source de champ magnétique, et donc aucun champ ne
peut exister à l'intérieur de ce métal. On a donc:
infinie. Aucune source de champ magnétique, et donc aucun champ ne
peut exister à l'intérieur de ce métal. On a donc:
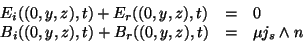
![]() et
et
![]() les champs
électriques et magnétiques d'une onde plane monochromatique. Le champ
magnétique réfléchis est donné par
les champs
électriques et magnétiques d'une onde plane monochromatique. Le champ
magnétique réfléchis est donné par
![]() et
et
![]() . L'onde résultante en tout point est donc égale
à:
. L'onde résultante en tout point est donc égale
à:
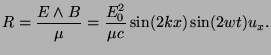
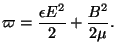
![]() et un plan d'incidence défini
par
et un plan d'incidence défini
par ![]() , l'on dira que:
, l'on dira que:
![]() heurtant une surface
heurtant une surface ![]() avec un angle d'incidence
avec un angle d'incidence ![]() . La
partie
. La
partie ![]() étant occupée par un métal parfait, on peut
montrer [Lum95] que l'onde réfléchie a pour équation :
étant occupée par un métal parfait, on peut
montrer [Lum95] que l'onde réfléchie a pour équation :