suivant: Couleur des matériaux
monter: Définition de la couleur
précédent: Définition de la couleur
Table des matières
Index
Le métamérisme
Nous avons vu dans les paragraphes précédents que calculer la couleur
associée à un spectre pouvait s'interpréter comme le calcul de la
projection de ce spectre dans un sous espace de dimension 3 appelé le
sous espace visuel humain. Le passage à un espace de dimension 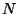 à un
espace de dimension 3 implique une perte d'informations dès que
à un
espace de dimension 3 implique une perte d'informations dès que 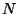 est
plus grand que 3 (ce qui est largement le cas). Il existe donc une
quantité de spectres différents possédant la même projection et donc
associés à la même sensation colorée. Ces spectres sont dits métamères.
est
plus grand que 3 (ce qui est largement le cas). Il existe donc une
quantité de spectres différents possédant la même projection et donc
associés à la même sensation colorée. Ces spectres sont dits métamères.
On peut donc se représenter l'ensemble des spectres comme deux
espaces orthogonaux :
- l'espace visuel humain de dimension 3 et
- un espace de dimension
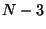 . Les spectres situés dans cet
espaces ne sont pas associés à une sensation colorée. Plus exactement,
un spectre défini dans cet espace donnera une sensation de noir. En
conséquence, cet espace est souvent appelé l'espace
noir.
. Les spectres situés dans cet
espaces ne sont pas associés à une sensation colorée. Plus exactement,
un spectre défini dans cet espace donnera une sensation de noir. En
conséquence, cet espace est souvent appelé l'espace
noir.
Si 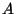 représente notre matrice d'appariement, la projection d'un
spectre quelconque sur le sous espace visuel humain est donné par
représente notre matrice d'appariement, la projection d'un
spectre quelconque sur le sous espace visuel humain est donné par
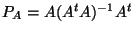 et la projection sur l'espace noir par
et la projection sur l'espace noir par 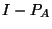 où
où 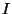 représente la matrice identité de
représente la matrice identité de 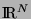 .
.
Tout spectre 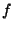 peut donc se décomposer en une partie visible et une partie
invisible :
peut donc se décomposer en une partie visible et une partie
invisible :
Le lecteur curieux peut vérifier que :
Les spectres possédant la même projection sur l'espace visuel
humain seront donc métamères. Etant donné un spectre 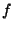 , l'ensemble de ses
métamères est égal à :
, l'ensemble de ses
métamères est égal à :





suivant: Couleur des matériaux
monter: Définition de la couleur
précédent: Définition de la couleur
Table des matières
Index
Brun Luc
2004-03-25
![]() représente notre matrice d'appariement, la projection d'un
spectre quelconque sur le sous espace visuel humain est donné par
représente notre matrice d'appariement, la projection d'un
spectre quelconque sur le sous espace visuel humain est donné par
![]() et la projection sur l'espace noir par
et la projection sur l'espace noir par ![]() où
où ![]() représente la matrice identité de
représente la matrice identité de ![]() .
.
![]() peut donc se décomposer en une partie visible et une partie
invisible :
peut donc se décomposer en une partie visible et une partie
invisible :