suivant: Constance chromatique
monter: Définition de la couleur
précédent: Le métamérisme
Table des matières
Index
Nous avons vu dans la section 2.2 que le spectre
renvoyé par un objet pouvait être décrit par sa fonction de
réflectance
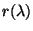 qui dépend de l'angle d'incidence de la
lumière, de l'angle de réflexion et des propriétés optiques du
matériel. Ces paramètres étant fixés, la couleur de l'objet est
définie par :
qui dépend de l'angle d'incidence de la
lumière, de l'angle de réflexion et des propriétés optiques du
matériel. Ces paramètres étant fixés, la couleur de l'objet est
définie par :
où 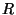 est une matrice
est une matrice 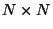 diagonale telle que la valeur du
diagonale telle que la valeur du
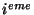 élément sur la diagonale est égal à
élément sur la diagonale est égal à
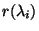 . Si l'on
develope cette dernière équation, l'on obtient:
. Si l'on
develope cette dernière équation, l'on obtient:
Une approximation, souvent effectuée en lancé de rayon, consiste à
calculer la couleur réfléchie par un blanc d'égale énergie (dont
l'énergie est constante sur chaque longueur d'onde) et à assimiler le
triplet obtenu à la reflectance sur chaque longueur d'onde. Cette
méthode calcule donc tout d'abord la couleur :
où 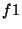 est un vecteur dont toutes les composantes sont égales à
1. Les composantes du vecteur
est un vecteur dont toutes les composantes sont égales à
1. Les composantes du vecteur 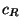 et celles de c sont ensuite
multipliées 2 à 2. Selon ce calcul, la lumière réféchie est donc égale
à
et celles de c sont ensuite
multipliées 2 à 2. Selon ce calcul, la lumière réféchie est donc égale
à
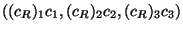 où
où
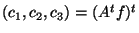 . Trancrit en terme de sommes, le calcul
précédent revient à assimiler :
. Trancrit en terme de sommes, le calcul
précédent revient à assimiler :
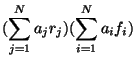
et
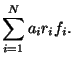
On confonds donc une somme de produits avec un produit de sommes. Cette
aproximation permet un gain de temps appréciable, puisque l'on travaille
uniquement avec des triplets de couleurs et non avec des spectres, mais
conduit à des résultats inacceptables dès que l'on veut obtenir des
images réalistes.





suivant: Constance chromatique
monter: Définition de la couleur
précédent: Le métamérisme
Table des matières
Index
Brun Luc
2004-03-25
![]() qui dépend de l'angle d'incidence de la
lumière, de l'angle de réflexion et des propriétés optiques du
matériel. Ces paramètres étant fixés, la couleur de l'objet est
définie par :
qui dépend de l'angle d'incidence de la
lumière, de l'angle de réflexion et des propriétés optiques du
matériel. Ces paramètres étant fixés, la couleur de l'objet est
définie par :
![]() est une matrice
est une matrice ![]() diagonale telle que la valeur du
diagonale telle que la valeur du
![]() élément sur la diagonale est égal à
élément sur la diagonale est égal à
![]() . Si l'on
develope cette dernière équation, l'on obtient:
. Si l'on
develope cette dernière équation, l'on obtient:
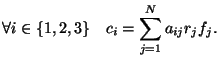
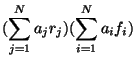 et
et