Définition de la couleur

Nous avons vu dans la section 3.2 que chaque cône, L, M ou S est sensible à une certaine plage de longueurs d'ondes. La sensibilité de chaque cône aux différentes longueurs d'ondes peut être décrite par trois fonctions $l(\lambda)$, $m(\lambda)$ et $s(\lambda)$ décrivant la sensibilité des cônes L, M et S à chaque longueur d'onde. La réponse d'un cône étant proportionnelle à la somme de ses excitations, la réponse $(c_1,c_2,c_3)$ des cônes L, M et S à un spectre $f(\lambda)$ donné peut être modélisée par:

$$\left \{ \begin{array}{lll} c_1 &=& \int_{360}^{830} l(\lamb... ...360}^{830} s(\lambda)f(\lambda)d\lambda.\\ \end{array}\right.$$

Si l'on échantillonne les fonctions $f$, $l$,$m$ et $s$, on peut considérer celles-ci comme des vecteurs de taille $N$. L'équation précédente peut donc se réécrire sous la forme :

$$\left \{ \begin{array}{lll} c_1 &=& \sum_{i=1}^{N} l(\lambda... ...\sum_{i=1}^{N} s(\lambda_i)f(\lambda_i).\\ \end{array}\right.$$

où $(\lambda_1,\dots,\lambda_n)$ représente nos $N$ échantillons. Si l'on pose :

$$S^t= \left( \begin{array}{lll} l(\lambda_1)&\dots&l(\lambda_... ...da_N)\\ s(\lambda_1)&\dots&s(\lambda_N)\\ \end{array}\right)$$

où $S^t$ représente la transposée de $S$, notre calcul intégral peut s'écrire sous la forme d'un produit matriciel:

$$c = S^tf.$$ (4.1)

Notez que les équations précédentes ne sont valides que si l'on suppose que tous les cônes de même type sont décris par les mêmes fonctions de réponse, non seulement pour tous les cônes d'un même individu mais pour deux individus différents. Le lissage réalisé entre les cônes de même type de la rétine permettent d'obtenir une réponse relativement similaire pour tous les cônes. De plus, des expériences ont montré que ces réponses variaient peu entre individus.

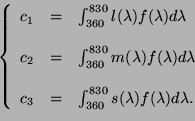
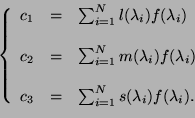
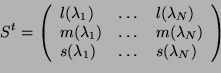
L'équation 4.1 peut se voir comme une projection du spectre $f$ sur le sous espace engendré par les vecteurs $l$, $m$ et $s$. Ce sous espace appelé Le sous espace Visuel Humain décrit la partie des spectres que nous sommes capables de percevoir. La quantité $S^tf$ décrit les coordonnées de la projection du spectre $f$ dans la base $l$, $m$, $s$ et peut s'interpréter comme une mesure de la sensation colorée lors de la perception du spectre $f$.

Le vecteur 3D $c=S^tf$ représentant la sensation colorée liée à la perception du spectre $f$, nous pourrions considérer que $c$ représente la couleur associée à $f$. Toutefois, la sensibilité des cônes $L$, $M$ et $S$ déterminée par les fonctions $l$, $m$ et $s$ est difficile à mesurer puisqu'elle nécessite de brancher des électrodes sur différents cônes d'un observateur humain. De plus, tout changement de base dans le sous espace Visuel Humain nous donnera une mesure équivalente de la couleur. Nous allons donc essayer de déterminer des bases permettant de calculer plus facilement les triplets représentant une couleur. Ces expériences sont appelées des mises en correspondance de couleurs.

Supposons que nous disposions de trois sources lumineuses $p_1$, $p_2$, $p_2$ colorimétriquement indépendantes telles que les trois vecteurs $S^tp_1$, $S^tp_2$ et $S^tp_3$ forment une base libre de $\RR^3$. Toute couleur $c=S^tf$ peut donc s'écrire comme une combinaison linéaire de ces trois vecteurs :

$$c=S^tf=\alpha_1(S^tp_1)+\alpha_2(S^tp_2)+\alpha_3(S^tp_3)$$

où $\alpha_1$, $\alpha_2$ et $\alpha_3$ appartiennent à $\RR$ et représentent les coorconnées de $c$ dans la nouvelle base. Cette dernière expression peut également d'écrire sous la forme:

$$c= S^tf=S^t(\alpha_1p_1+\alpha_2p_2+\alpha_3p_3)$$

Si l'on note par $P=(p_1,p_2,p_3)$ la $N\times 3$ matrice représentant les spectres de nos trois sources, l'on a :

$$c=S^tf=S^tP\left( \begin{array}{l}\alpha_1\\ \alpha_2\\ \alpha_3\end{array} \right)$$ (4.2)

La matrice $S^tP$ est une matrice $3\times 3$ dont les vecteurs colonnes sont égaux à $(S^tp_1,S^tp_2,S^tp_3)$. Ces trois vecteurs formant par hypothèse une base de $\RR^3$, la matrice $S^tP$ est inversible. Ainsi, l'impression colorée obtenue à partir d'une source lumineuse $f$ peut être reproduite par combinaison de trois sources lumineuses $p_1$, $p_2$, $p_3$ d'intensités relatives $\alpha(f)=(\alpha_1,\alpha_2,\alpha_3)$. La détermination des coefficients $\alpha(f)$ s'effectue à l'aide d'expériences d'appariement de couleurs : un sujet se voit présenté deux taches colorées (voir Figure 4.1) l'une obtenue à partir d'une source $f$ et l'autre grâce à une combinaison de trois sources $p_1$, $p_2$, $p_3$. Le sujet doit modifier les coefficients $\alpha$ de façon à ce que les deux taches colorées soient de couleur identique. Le triplet $(\alpha_1,\alpha_2,\alpha_3)$ vérifie alors l'équation 4.2.

color_matchingL'expérience d'appariement de couleurs

Le vecteur $\alpha(f)$ défini par l'équation 4.2 peut comporter une ou plusieurs composantes négatives. Ces coefficients ne peuvent donc pas être déterminés par l'expérience précédente où les sujets ne peuvent envoyer que des quantités positives de lumières sur l'écran. Dans ce cas, le sujet est autorisé à déplacer un ou plusieurs projecteurs $p_i$ de l'autre côté (voir Figure 4.2). Si l'on suppose que $\alpha_1$ est le coefficient négatif, ceci revient à faire l'appariement :

$$f - \alpha_1p_1= \alpha_2p_2+\alpha_3p_3.$$

On réalise alors un appariement avec uniquement des coefficients positifs.

color_matching2Appariement avec des couleurs négatives

L'équation 4.2 montre que si l'on connait les triplets correspondant à un ensemble de spectres, l'on peut connaître les triplets de n'importe qu'elle combinaison de ces spectres. En effet, si $(f_i)_{i\in\{1,\dots,n\}}$ représente un ensemble de spectres, chaque $f_i$ étant décrit par un triplet $\alpha(f_i)$, alors n'importe qu'elle combinaison de ces spectres $g=\sum_{i=1}^p \beta_if_i$ donnera une impression colorée définie par :

$$\begin{array}{llrl} S^tg &=& S^t&\sum_{i=1}^p \beta_if_i\\ &=... ...a(f_i)\\ &=&S^tP&\sum_{i=1}^p \beta_i\alpha(f_i).\\ \end{array}$$ (4.3)

On a donc $\alpha(g)=\sum_{i=1}^p \beta_i\alpha(f_i)$. Toute combinaison linéaire de spectres est décrite par la même combinaison de triplets associés.

Plutôt que déterminer expérimentalement les coefficients $\alpha$ de toutes les couleurs visibles, ce qui est matériellement impossible, on peut en utilisant la linéarité décrite dans le paragraphe précédent mesurer ces coefficients uniquement pour une base de $\RR^N$. Etant donnés les coefficients de chaque élément de cette base, l'on peut reconstruire n'importe quel spectre et donc obtenir son triplet associé par simple combinaison linéaire. Soit $(e_i)_{i\in\{1,\dots,N\}}$ la base canonique de $\RR^N$. Nous pouvons mesurer pour chaque $e_i$ le coefficient $a_i = \alpha(e_i)$ associé. On a donc pour tout $i$ appartenant à 1N :

$$S^te_i = S^tPa_i.$$ (4.4)

Ces $N$ équations peuvent s'écrire sous la forme matricielle suivante :

$$S^tI=S^tPA^t$$ (4.5)

où $I$ est la matrice identité de $\RR^N$ et $A=(a_1\dots a_N)$ est la matrice $3\times N$ définie par les vecteurs de coefficients $a_i$ de chaque vecteur unitaire $e_i$. Chaque coefficient $a_{ik}$ de la matrice $A$ représente la proportion de primaires $p_i$ nécessaire pour réaliser l'appariement du spectre $e_k$. La matrice $A$ est donc appelée la matrice d'appariement (ou color matching matrice). De même, les colonnes $a_i$ de A sont appelées les fonctions d'appariement (color matching functions).

De l'équation 4.5 nous pouvons déduire l'expression de A :

$$A= S(P^tS)^{-1}.$$

Le théorème suivant montre que la matrice $A$ peut être utilisée pour décrire les couleurs plutôt que $S$ :

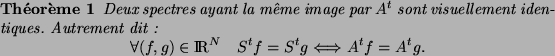
Nous pouvons donc indifférement exprimer des couleurs à l'aide de la matrice $S$ ou de la matrice $A$. La différence essentielle entre ces deux modes de représentation est que la matrice $S$ ne peut s'obtenir qu'avec des mesures extrêmement délicates de la sensibilité des cônes alors que la matrice $A$ peut s'obtenir à l'aide d'expériences d'appariements (voir Figures 4.1 et 4.2) nettement plus simples à réaliser.