Nous avons vu dans la section 4.1.1 que l'ensemble
des spectres pouvait être décomposer en deux espaces vectoriels
orthogonaux: L'espace visuel humain ![]() correspondant à la
partie visible de l'ensemble des spectres, l'espace noir
correspondant à la
partie visible de l'ensemble des spectres, l'espace noir
![]() correspondant à la partie invisible.
correspondant à la partie invisible.
Si nous utilisons trois spectres visibles comme base de l'espace visuel humain, il existera toujours des spectres ayant des coordonnées négatives sur cette base. Si nous utilisons par exemple l'espace ou les trois primaires sont vivibles la Figure 4.3 nous monre que les couleurs bleu-vert(450-550 nm) ne peuvent être reproduites par superposition des trois spectres. Ceci peut poser des problèmes dès que l'on désire travailler en synthèse additive (en n'ajoutant que des quantitées positives de couleur). La CIE à donc conçu un espace de couleur basé sur trois primaires X, Y et Z non visibles. Cet espace possède plusieurs propriétés intéressantes:
La transformation de l'espace à l'espace peut s'interpreter comme un changement de base donné par la matrice:

Un ensemble de vecteurs 3D étant difficile à manipuler, et à visualiser. Un façon élégante de résoudre ce problème consiste a projeter les veteurs 3D sur le plan unitaire (le plan sur lequel la somme des composantes est égale à 1). La somme des trois composantes ne représantant que l'intensité de la couleur et non la proportion de chacune des primaires, l'on obtient ainsi un diagrame appellé diagrame de chromaticité les projetions des vecteurs 3D représentant les couleurs étant appellées des coordonnées chromatiques.
Le diagramme de chromaticité sans doute le plus utilisé est le diagramme chromatique xy de la CIE. Les coordonnées chromatiques x et y sont obtenues à partir des coordonnées X, Y et Z par la transformation suivante:
![\begin{displaymath}
\begin{array}[center]{lll}
x &=& \frac{X}{X+Y+Z}\\
y &=& \frac{Y}{X+Y+Z}\\
z &=& \frac{Z}{X+Y+Z}\\
\end{array}\end{displaymath}](img522.png)
La courbe représentée sur la Figure 4.5 représente
l'ensemble des spectres monochromatiques et est appellée le spectrum locus. Soit
![]() les
coordonnées XYZ du spectre monochromatique
les
coordonnées XYZ du spectre monochromatique ![]() (pour i appartenant à
1N). Tout spectre
(pour i appartenant à
1N). Tout spectre ![]() étant une somme pondérée de
étant une somme pondérée de ![]() , on
à:
, on
à:
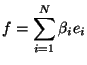
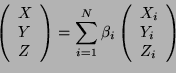
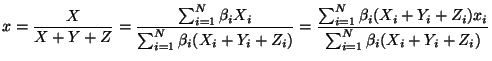
Notons enfin que l'espace ![]() (et plus précisément son plan
unitaire) est souvent utilisé pour désigner un espace couleur (voir
exercices sections 4.3.2,
4.3.3 ainsi que
4.4.2,
4.4.3). Les principaux avantages de ce
type de définition est de n'utiliser qu'un nombre réduit de valeurs et
de permettre une définition explicite du blanc de coordonnées
(et plus précisément son plan
unitaire) est souvent utilisé pour désigner un espace couleur (voir
exercices sections 4.3.2,
4.3.3 ainsi que
4.4.2,
4.4.3). Les principaux avantages de ce
type de définition est de n'utiliser qu'un nombre réduit de valeurs et
de permettre une définition explicite du blanc de coordonnées
![]() dans le nouvel espace.
dans le nouvel espace.