
Le prédicat
La segmentation d'une image en matériaux consiste à créer une partition de l'image en régions telle que chaque région soit composée d'un seul matériau. La segmentation d'une image est usuellement définie comme la partition de celle-ci en régions chaque région codant un objet de la scène. Une définition formelle d'un algorithme de segmentation a été donné par Horowitz et Pavlidis [HP76,HP75] en 1975.

Le prédicat ![]() est utilisé pour tester l'homogénéité des ensembles
est utilisé pour tester l'homogénéité des ensembles
![]() . Ces sous-ensembles constituent les régions de l'image. Une
segmentation de l'image est donc sa décomposition en un ensemble de
régions homogènes, le critère d'homogénéité
. Ces sous-ensembles constituent les régions de l'image. Une
segmentation de l'image est donc sa décomposition en un ensemble de
régions homogènes, le critère d'homogénéité ![]() restant à déterminer.
Zucker [Zuc76] a résumé les conditions de la
définition 8 comme suit : la première condition
implique que tout pixel de l'image appartienne à une région et une
seule. Cela signifie que l'algorithme de segmentation ne doit pas se
terminer avant d'avoir traité tous les points. La seconde condition
implique que toute région doit être connexe. La connexité des régions
étant induite par le voisinage défini sur l'image. La troisième
condition implique que chaque région doit être homogène. Enfin, la
quatrième condition est une condition de maximalité indiquant que la
fusion de deux régions ne doit pas être homogène. Il est important de
remarquer que le nombre
restant à déterminer.
Zucker [Zuc76] a résumé les conditions de la
définition 8 comme suit : la première condition
implique que tout pixel de l'image appartienne à une région et une
seule. Cela signifie que l'algorithme de segmentation ne doit pas se
terminer avant d'avoir traité tous les points. La seconde condition
implique que toute région doit être connexe. La connexité des régions
étant induite par le voisinage défini sur l'image. La troisième
condition implique que chaque région doit être homogène. Enfin, la
quatrième condition est une condition de maximalité indiquant que la
fusion de deux régions ne doit pas être homogène. Il est important de
remarquer que le nombre ![]() de régions formant la partition de l'image
reste indéterminé. Il peut donc exister plusieurs segmentations
possibles pour un prédicat
de régions formant la partition de l'image
reste indéterminé. Il peut donc exister plusieurs segmentations
possibles pour un prédicat ![]() donné.
donné.
Intuitivement un ``bon'' prédicat ![]() doit nous fournir une région
pour chaque objet de l'image. Toutefois, la notion d'objet est
généralement assez vague si bien que la problématique de la
segmentation est par essence mal définie. La segmentation en matériaux
au moins prise comme pré-traitement peut permettre une meilleure
définition du problème. La restriction de la problématique de la
segmentation à une segmentation en matériaux possède en effet deux
avantages fondamentaux :
doit nous fournir une région
pour chaque objet de l'image. Toutefois, la notion d'objet est
généralement assez vague si bien que la problématique de la
segmentation est par essence mal définie. La segmentation en matériaux
au moins prise comme pré-traitement peut permettre une meilleure
définition du problème. La restriction de la problématique de la
segmentation à une segmentation en matériaux possède en effet deux
avantages fondamentaux :
La majorité des algorithmes de segmentation en matériaux sont basés sur les modèles de Shafer [Sha85] ou Healey [Hea89] (Section 2.2.5). Nous allons dans cette Section établir les fondements de ces méthodes.
Le modèle de Shafer [Sha85](Section 2.2.5) exprime l'irradiance sur un capteur de la caméra par la somme d'une composante Lambertienne et d'une composante Spéculaire :
Étant donné une caméra couleur, la couleur d'un pixel ![]() se
déduit de l'irradiance sur ses capteurs par :
se
déduit de l'irradiance sur ses capteurs par :
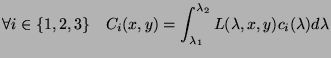
Si nous reprenons l'équation 6.5 nous obtenons :
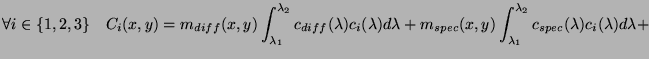
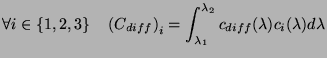 et
et 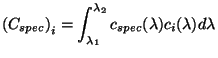
![]()
Le modèle de Healey est basé sur une décomposition supplémentaire en métaux et diélectriques. On obtient en en effet à partir de l'équation 2.20 :
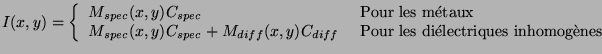
Klinker [HSW92a] a affiné cette description en remarquant que
dans le cas d'un diélectrique non homogène les points tels que le
vecteur ![]() n'est pas négligeable correspondent à des zones de
l'image fortement illuminées. De tels points correspondent à des zones
très localisées dans l'image pour lesquelles on peut négliger les
variations de la composante diffuse. Si nous nous référons au modèle
de Nayar (Section 2.2.4). Un telle approximation,
revient à négliger les variations de la composante Lambertienne
lorsque le lobe spéculaire ou le pic spéculaire n'est pas négligeable.
n'est pas négligeable correspondent à des zones de
l'image fortement illuminées. De tels points correspondent à des zones
très localisées dans l'image pour lesquelles on peut négliger les
variations de la composante diffuse. Si nous nous référons au modèle
de Nayar (Section 2.2.4). Un telle approximation,
revient à négliger les variations de la composante Lambertienne
lorsque le lobe spéculaire ou le pic spéculaire n'est pas négligeable.
![]()
La répartition des couleurs dans le parallélogramme de Shafer n'est
donc pas uniforme mais suit une distribution similaire à celle
représentée sur la Figure 6.2. L'ensemble des
couleurs d'un diélectrique non homogène dans des régions non hautement
éclairées peut donc être décrit uniquement par le vecteur
![]() . Dans le cas d'une zone de l'image hautement illuminée la
composante de ce vecteur sur
. Dans le cas d'une zone de l'image hautement illuminée la
composante de ce vecteur sur ![]() reste constante (valeur
reste constante (valeur
![]() sur la Figure 6.2) alors que les
variations se produisent sur le vecteur
sur la Figure 6.2) alors que les
variations se produisent sur le vecteur ![]() . L'histogramme des
couleurs d'un matériau a donc la forme d'un
. L'histogramme des
couleurs d'un matériau a donc la forme d'un ![]() renversé et légèrement
distordu. On peut également obtenir un histogramme en
renversé et légèrement
distordu. On peut également obtenir un histogramme en ![]() si
si ![]() est égal à la valeur maximum
est égal à la valeur maximum ![]() sur l'axe
sur l'axe ![]() . Une
étude de l'illumination d'un cylindre à amené
Klinker [HSW92a] à conclure que le seuil
. Une
étude de l'illumination d'un cylindre à amené
Klinker [HSW92a] à conclure que le seuil ![]() ne pouvait
se trouver que dans la seconde moitié de l'intervalle des variations
ne pouvait
se trouver que dans la seconde moitié de l'intervalle des variations
![]() . Cette hypothèse confirmée par des expériences sur des
images réelles est appelée l'hypothèse des 50% supérieurs. Nous
appellerons respectivement les lignes définies par
. Cette hypothèse confirmée par des expériences sur des
images réelles est appelée l'hypothèse des 50% supérieurs. Nous
appellerons respectivement les lignes définies par ![]() et
et
![]() la ligne diffuse et la ligne
spéculaire.
la ligne diffuse et la ligne
spéculaire.
Cette modélisation de l'ensemble des couleurs d'un matériau nous
permet d'interpréter l'ensemble des couleurs du voisinage d'un
point. En effet, étant donné un pixel de l'image et un fenêtre centrée
sur celui-ci, l'ensemble des couleurs des pixels contenus dans cette
fenêtre peut avoir une dimension 0, ![]() ,
, ![]() ou
ou ![]() . La dimension de
cet ensemble de couleurs peut être testée en utilisant les valeurs
propres de la matrice de covariance de l'ensemble de couleurs
(Section 5.2.1, équation 3).
. La dimension de
cet ensemble de couleurs peut être testée en utilisant les valeurs
propres de la matrice de covariance de l'ensemble de couleurs
(Section 5.2.1, équation 3).
Klinker [HSW92a] utilise cette classification pour décomposer l'image en matériaux. Schématiquement, sa méthode de segmentation se déroule de la façon suivante.
Notons que les pixels de dimensions 0 et ![]() ne sont pas
directement utilisés par l'algorithme. En effet l'information liée à
ces pixels est difficilement exploitable et ces pixels sont absorbés
par les étapes de croissance de région dans des régions de dimension
ne sont pas
directement utilisés par l'algorithme. En effet l'information liée à
ces pixels est difficilement exploitable et ces pixels sont absorbés
par les étapes de croissance de région dans des régions de dimension
![]() ou
ou ![]() .
.
La méthode présenté par Klinker utilise une approche ascendante. Healey [Hea95] a présenté une méthode comparable basée sur une approche descendante.
La méthode d'Healey néglige initialement la composante spéculaire des diélectriques inhomogènes. On a donc pour les métaux comme pour les diélectriques une équation de la forme :
Donné les fonctions de sensibilité
![]() de la caméra,
la couleur
de la caméra,
la couleur
![]() d'un pixel est donnée par :
d'un pixel est donnée par :
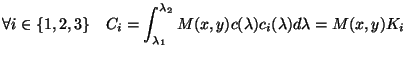 avec
avec 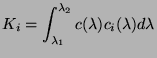
Si nous normalisons les coordonnées de chaque pixel par sa norme dans
![]() nous obtenons :
nous obtenons :
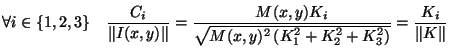
La segmentation d'une image se ramène donc à une reconnaissance de
droites dans l'espace couleur ou à la reconnaissance d'un ensemble de
distributions normales dans l'espace normalisé par ![]() . C'est cette
dernière option que choisi Healey. Un matériau
. C'est cette
dernière option que choisi Healey. Un matériau ![]() est caractérisé
par sa moyenne
est caractérisé
par sa moyenne ![]() et sa matrice de covariance
et sa matrice de covariance ![]() (Section 5.2.1, équation 3). La
distribution des couleurs dans le matériau est alors modélisée par la
distribution normale
(Section 5.2.1, équation 3). La
distribution des couleurs dans le matériau est alors modélisée par la
distribution normale
![]() définie par
définie par
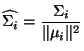
Donné la modélisation de chaque matériau, la classification d'une
couleur ![]() a un matériau parmi
a un matériau parmi ![]() s'effectue en utilisant les
fonctions suivantes basées sur la théorie de la décision de
Bayes [DH73] :
s'effectue en utilisant les
fonctions suivantes basées sur la théorie de la décision de
Bayes [DH73] :
Si nous supposons que tous les matériaux sont équitablement
représentés ![]() devient indépendant de
devient indépendant de ![]() et l'équation précédente
peut se simplifier en :
et l'équation précédente
peut se simplifier en :
Donné cette méthode de classification, Healey commence par appliquer un opérateur gradient sur l'image. L'idée sous-jacente est de caractériser les zones correspondant à seul matériau comme des zones de faible gradient. Notons toutefois que cette supposition est discutable. En effet, l'opérateur gradient va non seulement réagir à des changements de matériaux mais également à de brusque changement de géométrie sur un objet composé d'un seul matériau.
Donné l'image de gradient Healey décompose l'image à l'aide d'un quadtree [CP95] et initialise une liste vide de matériaux. Tout noeud du quadtree couvrant une zone de l'image de faible gradient est supposé composé d'un seul matériau. Healey calcule donc sa couleur moyenne normalisée :
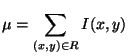
La moyenne ![]() est alors comparée aux
est alors comparée aux ![]() matériaux présents
dans la liste à l'aide de l'équation 6.7. Si la
valeur maximum de
matériaux présents
dans la liste à l'aide de l'équation 6.7. Si la
valeur maximum de
![]() est supérieure à un seuil
est supérieure à un seuil ![]() la
région est affectée à un des matériaux de la liste. Sinon Healey
considère que la région est composée d'un nouveau matériau et celui-ci
est ajouté à la liste en utilisant les données de la région
la
région est affectée à un des matériaux de la liste. Sinon Healey
considère que la région est composée d'un nouveau matériau et celui-ci
est ajouté à la liste en utilisant les données de la région ![]() .
.
La méthode de Healey segmente donc l'image en un ensemble de régions, tel que l'ensemble des couleurs de chaque région décrit une droite dans l'espace de couleurs. Il convient ensuite de fusionner les régions adjacentes composée d'un seul matériau telle que l'une des régions correspond à la droite diffuse tandis que l'autre correspond à la droite spéculaire. Schématiquement, une fusion est réalisée entre deux régions si :
La méthode de Healey repose donc sur une découpe récursive de l'image afin d'obtenir des patchs de surface composés d'un seul matériau. Malgré l'approche différente de celle de Klinker, ces deux méthodes sont basés sur les mêmes idées de base :